Equilibrium and Center of Gravity problem

[p0ke]

I'm having some trouble finding a definitive answer for this problem of my physics lab.

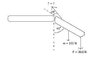
The large quadricep muscles in the upper leg terminate at the lower end in a tendon attached to the upper end of the tibia. The force on the lower leg when the leg is extended are modeled below (attached jpg), where T is the tension in the tendon, w is the force of gravity acting on the lower leg, and F is the weight of the foot. Find T when the tendon is at an angle of 20 degrees with the tibia, assuming that w = 180N, F = 30.0 N, and the leg is extended at an angle of 45.0 degrees with the vertical. Assume that the center of gravity of the lower leg is at its center, and that the tendon attaches to the lower leg at a point one fifth of the way down the leg.

I've been looking through some examples to try to come up with a general idea, but this problem seems somewhat different as no lengths or distances are given except that the tendon attaches 1/5 down the leg. So far, I've found forces in x and y components to get

SUMFx = Tx + wx + Fx = 0
to get Tx = 0.
Then in y direction, I'm not sure if i can do this but i found
Tsin65 - 180 - 30 = 0
to get T = 231.7.

Knowing that this is supposed to be a torque-related problem I also used SUMt = tT + tw + tF = 0. Then tT = rTTsinθ. This is where I am stuck. How would I use the torque equilibrium equation if I am not given any distances? Any hints or suggestions would be really helpful!

 

[andrevdh]

Welcome to PF p0ke.

The length of the leg will appear in the calculation of all three torques. So you can cancel it out in "the sum of the torques = to zero". You can then take moments about the knee (pivot point) taking $$l$$ as the length of the tibia, which then cancels in the equation. The only unknown in the torque equation will then be the tension in the muscle. So you only need to consider this equation. There will also be a reaction force at the knee acting on the tibia, which need not be included in the torque equation if you take the torques about the knee.

 

[kyle8921]

I would suggest approaching this problem by first drawing a free body diagram of the lower leg. This will help visualize the forces acting on the leg and determine the direction of these forces. From the given information, we know that the force of gravity (w) and the weight of the foot (F) act downwards, and the tension in the tendon (T) acts upwards at an angle of 20 degrees with the tibia.

Next, we can use the equations for force and torque equilibrium to solve for the unknown tension (T). In the x-direction, we have:

Tx - wx - Fx = 0

Since we are given that the tendon attaches one fifth of the way down the leg, we can assume that the distance between the center of gravity and the point of attachment is one fifth of the length of the leg. This means that Fx = (1/5)F. Substituting in the given values, we get:

Tx - 180sin45 - (1/5)F = 0

Solving for Tx, we get Tx = 180sin45 + (1/5)F = 180sin45 + 6.

In the y-direction, we have:

Ty + wy + Fy = 0

Substituting in the given values and solving for Ty, we get:

Ty = -180cos45 - 30 = -180cos45 - 30.

Now, we can use the torque equilibrium equation to solve for T. We know that the torque of the tension in the tendon is equal to the distance between the point of attachment and the center of gravity (1/5 of the length of the leg) multiplied by the magnitude of the tension (T) multiplied by the sine of the angle between the tension and the lever arm (20 degrees). This can be represented as:

Tsin20 = (1/5)(length of leg)(T)sin20

Substituting in the values and solving for T, we get T = 180sin45 + 6.

Therefore, the tension in the tendon (T) is equal to 180sin45 + 6 = 237.1 N.

I hope this helps with solving the problem. Remember to always draw a free body diagram and use the equations for force and torque equilibrium to solve for unknowns.