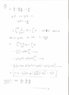CAF123
Gold Member
- 2,918
- 87
Homework Statement
A particle of mass ##m## is projected from ##x(0) = x_o## in the vertical direction, with an initial velocity, ##\dot{x}(0) = v_o##. It is subject to gravity and linear drag, mk|v|, against the motion.
1) Show that the body follows ##v(t)## such that:$$v(t) = -g/k + (v_o + g/k)e^{-kt}$$
2) Use ##\ddot{x} = v dv/dx ## to find a soln to the motion subject to the initial condition. Show the equivalence between the result attained and the one shown in 1).
Homework Equations
Separable Diff Eqns, Newton 2nd
The Attempt at a Solution
1) is fine. I don't really know how to show the equivalence, but I have tried two different ways, where one way I get nothing near equivalence and the other I recover the exp term above, but not the -g/k in front.
Method 1). After solving ##\ddot{x} = v dv/dx, ##I get ##x = x(v)##. Then by the chain rule, ##dx/dt = dx/dv\,dv/dt##. So I differentiated my soln in 2) wrt v and then multiplied this by the derivative of v wrt t in 1). This gives me nothing near equivalence, although I am not sure why.
Method 2). Put v = v(t) in 1) into my x(v). This gives x(t). Then simply differentiate wrt t. I get the second term in 1) (exp term) but not the -g/k.
Both methods seem valid, (are they?) but I don't get the result. I could recheck my algebra again, but both methods yield a (g +kv)^3 and that is not present in 1) and it doesn't cancel.
Many thanks.