Equivalent Capacitance Question

[theskyisgreen]

Homework Statement

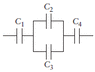
What is the equivalent capacitance of the four capacitors in the figure below? Take C1 = 2.6 µF, C2 = 4.1 µF, C3 = 3.9 µF, and C4 = 1.1 µF.

Homework Equations

Cequiv of capacitor in series = (1/C1)+(1/C2)+(1/C3)+(1/C4)
Then take the reciprocal of the answer.

The Attempt at a Solution

I actually happen to know that the answer is 0.705 but I can't figure out how exactly to get that answer. I have tried everything from plugging the numbers directly into the equation above and almost every combination I could think of.
It's frusterating because I think it's a simple question but I can not get the right answer using my methods. If anyone can help that would be great, thank you.

 

[Ry122]

Did you add c2 and c3 as if they're resistors in series?
after doing that, pretend that value represents a new capacitor at that same location. and add that capacitor to c4 and c1 as if they're resistors in parallel.

 

[rl.bhat]

Cequiv of capacitor in series = (1/C1)+(1/C2)+(1/C3)+(1/C4)

In this problem the above formula is not relevant because it has a combination of series and parallel circuits. The formula becomes

1/Ceff = 1/C1 + 1/(C2+C3) + 1/C4

Now find Ceff.