Equivalent Capicitance (with a resistor)

[Fluent]

Hello, I came across a type question and my prof never went through it in the class and unfortunately I couldn't find it in the textbook nor on the internet.

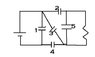
I can find the equivalent capicitance of capacitors in a combination of series/parallel no problem, however when a resistor is thrown in I am completely lost. I came across this problem on a test, I will show the picture. I do not remember the numbers, however this is what the picture looked like.

Now when I simply ignored the resistor to find the equivalent capacitance (only way I could think to try it) my answer didn't exactly match one of the possible answers. Could you please let me know what I need to be doing? because simply combining capacitors was not working for me.

Thanks in advance.

Edit: What was given in the question: The Emf voltage, all the capacitances, and the resistance of the resistor. If it helps to assign numbers to show me, I added in numbers so you may do that.

 

[vanesch]

The simple answer is that such a circuit, in all generality, doesn't have an equivalent capacitance, meaning that you cannot think up a single capacity value that a capacitor would have, and that would behave in all circumstances in the same way as this circuit.

I don't know if you've learned already about impedance and about the frequency dependence of impedance, but to keep it short, the impedance is given by the ratio of (complexified) voltage over (complexified) current for a sinusoidal voltage as a function of the frequency.

A capacitor has a specific impedance which is purely imaginary and goes like - i /( C 2 pi f )
where i is the complex i. A resistor is the only kind of impedance which is purely real and independent of frequency: it's impedance is its resistor value (say, 100 ohms or so).
A self has a specific impedance which is also purely imaginary, but goes like i 2 pi f L this time.

So all these are complex numbers which are function of frequency.

Well, for your circuit, I didn't do the calculation, but I have enough experience to tell you that its frequency dependence won't vary in 1/f nor will it be purely imaginary, so you won't be able to find a single number C for which the impedance of the circuit can be written -i / (C 2 pi f). And that means that it doesn't have an "equivalent capacitance".

A circuit just made up of capacitors DOES have such a dependence, and there you CAN find such a number C, and it is the number you usually call "equivalent capacitance" (with the rules for parallel and series and so). But once you mix in resistors or selfs, that won't, in general, be the case.

Now, it could be that one is asking for a LIMIT CASE. For instance, what is the equivalent capacitance IN DIRECT CURRENT ? Or what is the equivalent capacitance at high frequencies ?

Then you have to find the asymptotic behavior of the impedance, and see if it has a 1/f behavior near f = 0, or for very large f.

You could also directly try to write the differential equations of the circuit and try to solve it, for a given sollicitation.

BTW, I move this to "homework". We usually delete homework posted in the other forums, but as this is a border case (discussion or really homework) I moved it.

 

[Fluent]

That's very odd.. This is a General Physics course and as the semester is over we won't be learning about any of that complex stuff. Maybe there's some assumptions that he expected us to make in order to solve it.

Thanks for the input.