Equivalent circuit of induced EMF of coil.

[yungman]

I want to model a coil circuit with induced EMF. I want to verify that my model is correct in a circuit. That the voltage developed across the load is calculated correctly. From the equivalent circuit, you can see the current depend on the jX_L and it acts as a low pass filter in the complete circuit loop because the value increase and cause less voltage develop across the Load.

Let coil:

Z_L=R_L+jX_L

Maxwell eq. For EMF induction:

\nabla\times \vec E =-\frac {\partial \vec B}{\partial t}\;\Rightarrow\; \int_S \nabla \times \vec E\;\cdot\;d\vec S = \int_C \vec E\cdot d \vec l = -\frac{\partial}{\partial t}\left(\int_S \vec B \cdot d\vec S\right)=-\frac{\partial \Phi}{\partial t}

Where \Phi\; is the magnetic flux. Therefore induced EMF:

V_{IND}= \int_S \nabla \times \vec E\;\cdot\;d\vec S = \int_C \vec E\cdot d \vec l = -\frac{\partial}{\partial t}\left(\int_S \vec B \cdot d\vec S\right)=-\frac{\partial \Phi}{\partial t}

To put the whole thing together, using the coil to drive the load, the total equivalent circuit is shown with the \;V_{IND}\; modeled as an ideal voltage source:

146972[/ATTACH]"]

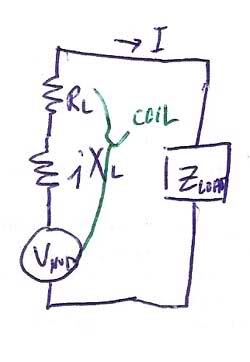
where I use Z_L=R_L+jX_L and the current in the loop is:

I= \frac {V_{IND}}{R_L+jX_L+R_{LOAD}}\;\hbox { and }\; V_{LOAD}=I\;R_{LOAD}

I updated that the load is a pure resistance, not reactance, or else it can really get dicey!

Thanks

Alan

 

[jim hardy]

golly your math is awesome to a plodder like me.

looks quite rigorous.

2 dumb questions come to mind but i'll bet you've got them both covered.
what's the core made of?
how well is B defined ?

core losses would resemble another resistor in parallel with coil so hopefully either it's air core or flux is low enough you won't have to deal with messy old iron loss (b*f^1.4).

and hopefully the load current isn't enough to reach back and perturb B through Xl's own amp-turns.

wow. somebody actually understands those DEL's? i need to go back to school...

humbly,

old jim

 

[yungman]

Hi Jim, thanks for your reply. It is an air core, but it could be quite high inductance and wire resistance. In some case, the wire resistance can be up to 6KΩ. I don't think( I sure hope not) the equivalent parallel resistance come to play and relatively low freq of less than 50KHz. The B is undefined, it is used as a sensor!

To clarify, I want to nail the current in relation of the load and the characteristic of the coil. I should simplify a little and make the load a pure resistance with no reactance.

The equation is only to show that the flux through the coil induce a voltage, not a current, and that's the reason why I arrive my assumption of an ideal voltage source. It is not necessary for the modelling as long as you accept the voltage source notion. My point is I can model the induced EMF of the coil by an ideal voltage source in series with it's reactance, internal resistance and the load resistance. That the load voltage can be calculated by simple voltage division of a series circuit.

Thanks

Alan

 

[jim hardy]

""It is an air core, but it could be quite high inductance and wire resistance. In some case, the wire resistance can be up to 6KΩ. I don't think( I sure hope not) the equivalent parallel resistance come to play and relatively low freq of less than 50KHz. The B is undefined, it is used as a sensor!""

ahhh that's what you're doing! a flux detector...

well with air core there'll sure be no iron losses.

i did something similar, mentioned in another thread, but mine was much simpler because 60 hz was only frequency of interest. But it did track down RFI from a microwave link that was upsetting the security guys' metal detector .

two effects i'd test for in prototype:

Resonance: it sounds like you're using a lot of wire. that coil will have a natural frequency because of inter-turn capacitance, and i'd think near that frequency you'll suffer the voltage gain of a series resonant circuit. Maybe it'll be well above your 50khz.

armature reaction : load current will cause flux that counters the flux you're trying to measure, reducing the induced voltage. Maybe your modelling ideal voltage source and Xl will calculate out that effect - i don't know.
For that reason i used my flux detector with a high impedance scope probe.

is this why you're building that driver in thread ""Need opinion of phase compensation for inductor. "" ??

old jim

 

[es1]

I want to model a coil circuit with induced EMF.

I am a little confused. Isn't that what the secondary side of a transformer looks like? Maybe just use a standard transformer mathematical model and tweak the constants, and source at the primary, to fit your application.

 

[yungman]

I am a little confused. Isn't that what the secondary side of a transformer looks like? Maybe just use a standard transformer mathematical model and tweak the constants, and source at the primary, to fit your application.

Similar, but this is variable frequency, and the high inductance cause output amplitude to change with frequency within the working range. That's the reason I need to create a correct model to predict the output behavior. It is not as if I can intentionally design a coil with low enough inductance and resistance to knock those variables out. I have to live with all these.

I am not very good with transformers either, so that does not help.

 

[yungman]

""It is an air core, but it could be quite high inductance and wire resistance. In some case, the wire resistance can be up to 6KΩ. I don't think( I sure hope not) the equivalent parallel resistance come to play and relatively low freq of less than 50KHz. The B is undefined, it is used as a sensor!""

ahhh that's what you're doing! a flux detector...

well with air core there'll sure be no iron losses.

i did something similar, mentioned in another thread, but mine was much simpler because 60 hz was only frequency of interest. But it did track down RFI from a microwave link that was upsetting the security guys' metal detector .

two effects i'd test for in prototype:

Resonance: it sounds like you're using a lot of wire. that coil will have a natural frequency because of inter-turn capacitance, and i'd think near that frequency you'll suffer the voltage gain of a series resonant circuit. Maybe it'll be well above your 50khz.

armature reaction : load current will cause flux that counters the flux you're trying to measure, reducing the induced voltage. Maybe your modelling ideal voltage source and Xl will calculate out that effect - i don't know.
For that reason i used my flux detector with a high impedance scope probe.

is this why you're building that driver in thread ""Need opinion of phase compensation for inductor. "" ??

old jim

Yes, there is always a resonance at about 6KHz. I really don't know exactly how to model, I am just trying to make up a model to predict the current change so I can compensate in the later stage. As in most cases, designing the circuit is the easy part, modelling the problem is really the hard part.

Isn't like closed loop feedback control system, designing the poles and zero is the easy part, nailing the system poles and dead time is really the key and the hard part! In my case, all the interaction is in the frequency of interest, I cannot just use the equivalent of dominant pole compensation to drown out the secondary effect!

 

[jim hardy]

well your approach resembles thevenin's equivalent , so it sure appears rooted in sound principles.

it'll be easy enough to check.

build one
measure its L and R
excite it with external field from an AC solenoid
measure open circuit voltage
measure short circuit current

does it behave like measured open circuit voltage in series with measured L and R ?

i'll be real curious to hear if you do that experiment.

as you said, ".. modelling the problem is really the hard part."

 

[yungman]

well your approach resembles thevenin's equivalent , so it sure appears rooted in sound principles.

it'll be easy enough to check.

build one
measure its L and R
excite it with external field from an AC solenoid
measure open circuit voltage
measure short circuit current

does it behave like measured open circuit voltage in series with measured L and R ?

i'll be real curious to hear if you do that experiment.

as you said, ".. modelling the problem is really the hard part."

Thanks, you reminded me about the inter winding capacitance that I forgot, that is going to make things even more complicated, I have to think about how to incorporate into the model. That, at least I can measure.