danielakkerma
- 230
- 0
Hi all!
Having decided to return to coding some of the physical problems that I require solving(in lieu say, of Mathematica), I endeavored to adapt the Crank-Nicolson to my needs, but, in order to test my algorithm, I had first attempted to resolve the common and trivial heat equation, in one dimension, e.g \alpha\frac{\partial^2u}{\partial x^2} = \frac{\partial u}{\partial t}, with some plain boundary conditions, that is u(x, 0) = some trivial function(sine times cosine) and u(0, t) = 10(or some value), and at the end-point(10, t in this case), the same(essentially a rod kept at both ends at an equal temperature).
The results however, are unsatisfactory; For sake of my equation, I used:
\beta u^{i+1}_{j+1}+(1+2\beta)u^{i+1}_{j}+\beta u^{i+1}_{j-1}=u^{i}_{j}
Where beta is a constant derived from my step sizes(i.e, dx, dt) and i & j denote the step in time and displacement respectively.
This, as is well known, creates a tridiagonal system, which is readily evaluated for all U(i+1)ns(in my case, I've got a grid with a size of 100 units).
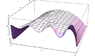
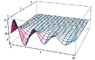
I've attached two graphs corresponding to the solutions; Image2 was created by Mathematica, and Image1 is done using my program. You can see the very disturbing groove that's created, that seems to wedge and ebb towards the margins of the computational region. This is, first-and-foremost, physically inaccurate, and should not occur, and in fact, using Mathematica, does not.
In short, I am reliant on your aid to solve this discrepancy,
I thank you for your attention,
Beholden,
Daniel
Having decided to return to coding some of the physical problems that I require solving(in lieu say, of Mathematica), I endeavored to adapt the Crank-Nicolson to my needs, but, in order to test my algorithm, I had first attempted to resolve the common and trivial heat equation, in one dimension, e.g \alpha\frac{\partial^2u}{\partial x^2} = \frac{\partial u}{\partial t}, with some plain boundary conditions, that is u(x, 0) = some trivial function(sine times cosine) and u(0, t) = 10(or some value), and at the end-point(10, t in this case), the same(essentially a rod kept at both ends at an equal temperature).
The results however, are unsatisfactory; For sake of my equation, I used:
\beta u^{i+1}_{j+1}+(1+2\beta)u^{i+1}_{j}+\beta u^{i+1}_{j-1}=u^{i}_{j}
Where beta is a constant derived from my step sizes(i.e, dx, dt) and i & j denote the step in time and displacement respectively.
This, as is well known, creates a tridiagonal system, which is readily evaluated for all U(i+1)ns(in my case, I've got a grid with a size of 100 units).
I've attached two graphs corresponding to the solutions; Image2 was created by Mathematica, and Image1 is done using my program. You can see the very disturbing groove that's created, that seems to wedge and ebb towards the margins of the computational region. This is, first-and-foremost, physically inaccurate, and should not occur, and in fact, using Mathematica, does not.
In short, I am reliant on your aid to solve this discrepancy,
I thank you for your attention,
Beholden,
Daniel