Escape Velocity depends on the Radius of the Earth?

[Muhammad Danish]

We have 2 different formulas for escape velocity.

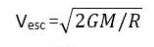and

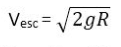. If we look at the first formula we see that escape velocity is inversely proportional to the square root of Radius of Earth. While in the second formula, escape velocity is directly proportional to the square root of Radius of Earth.

We know that escape velocity depends on the Radius of Earth. Which one will show its proper dependence? Is it directly proportional or inversely proportional?

 

[Ibix]

Does $g$ depend on $R$?

 

They're basically the same formula; how do you write $g$ in terms of $G$, $M$ and $R$?

But to answer your question, to find the dependence of one quantity ($V_{esc}$) on another ($R$), you have to write a relationship between them using only other quantities which are independent of those two things.

It's up to you to tighten the parameters of the question a little bit: i.e. is the density of the planet assumed constant?

 

[Muhammad Danish]

Does $g$ depend on $R$?

Yes. It is inversely proportional to square of radius. So if radius would increase, g would decrease and as a result V will decrease. While on the other hand if radius increases, V decreases. So ultimately V should be inversely proportional to the square root of R. Right?

 

Yes. It is inversely proportional to square of radius. So if radius would increase, g would decrease and as a result V will decrease. While on the other hand if radius increases, V decreases. So ultimately V should be inversely proportional to the square root of R. Right?

Use some algebruh! You might also say that $M(R) = \frac{4}{3}\pi R^3 \rho$... or if the density is not uniform it gets more complicated...

 

[Muhammad Danish]

Use some algebruh! You might also say that $M(R) = \frac{4}{3}\pi R^3 \rho$... or if the density is not uniform it gets more complicated...

Thank you so much! It was so confusing to me. My doubts are clear now. Thanks again!

 

[PeroK]

Thank you so much! It was so confusing to me. My doubts are clear now. Thanks again!

This is a common theme to look out for. For example, for uniform circular motion we have:
$$a = \frac{v^2}{R} = \omega^2 R$$
So, if you ask "how does acceleration depend on radius?", then it depends what other factors are held constant:

If velocity is constant, then acceleration is inversely proportional to radius;
If angular velocity is constant, then acceleration is proportional to radius.

You always have to ask yourself what quantities are fixed and what quantities are varying.

 

[Mikestone]

Or to put it another way, the Escape Velocity from the surface of a planet always equals he velocity (neglecting air resistance) at which a body would impact the surface after falling from an altitude equal to the planet's radius at a constant acceleration equal to the planet's surface gravity.

By a well-known theorem, if V = Escape velocity (ie the final velocity of an object falling from infinity),
R = the radius of the planet and G = acceleration due to gravity, then V = sqrt(2GR)

But reverting to grammar school physics, if a body is falling under a *constant* acceleration G then V= Gt where t = time taken to fall, and D = (Gt^2)/2 where D = the distance of fall.

So if sqrt(2GR) = Gt then 2GR = (Gt)^2 and R = (Gt^2)/2

Hence D = R.

So escape velocity is determined by the surface gravity and the radius.

 

[vanhees71]

You can also argue with the energy. With the usual choice of the gravitational potential (going to 0 at infinity), $$\Phi=-\frac{G m_1 m_2}{r}$$
The minimal energy for an unbound orbit is $E=0$
$$\frac{m_2}{2}v^2-\frac{G m_1 m_2}{r}=0,$$
with the radius of the Earth, $R$
$$v=\sqrt{\frac{2 G m_2}{R}}.$$
Now the gravitational acceleration on the surface of the Earth is
$$g=\frac{G m_2}{R^2}$$
and thus
$$v=\sqrt{2gR}.$$

 

[PeroK]

Or, the potential difference between the surface and infinity is:
$$V = \frac{GM}{R}$$
And, in the constant gravity model, the potential at a height $h$ is given by:
$$V = gh = \frac{GM}{R^2}h$$
These are equal when $h = R$.

 

[Mikestone]

$$V = \frac{GM}{R}$$
And, in the constant gravity model, the potential at a height $h$ is given by:
$$V = gh = \frac{GM}{R^2}h$$
These are equal when $h = R$.

There seem to be a lot of hash and dollar signs in some posts. Are they mathematical symbols or is my computer rendering them wrongly?

 

[PeroK]

There seem to be a lot of hash and dollar signs in some posts. Are they mathematical symbols or is my computer rendering them wrongly?

That's Latex. You should see them in mathematical form. Not sure why there would be a problem. You don't need anything special in your browser.

 

[Ibix]

Are they mathematical symbols or is my computer rendering them wrongly?

They're delimiters for LaTeX. The stuff between them ought to be interpreted by a Javascript package called MathJax abd shown to you as nicely rendered maths. You shouldn't need to do anything for this to happen - the maths should just render a second or two after the page loads. So $$F=\frac{GMm}{r^2}$$should appear as Newton's law of gravity. Try the usual stuff (refresh, close your browser and reopen) if you don't see it - it's really important for this site...

 

[Mikestone]

Thanks. Things seem to be working ok on Google Chrome.