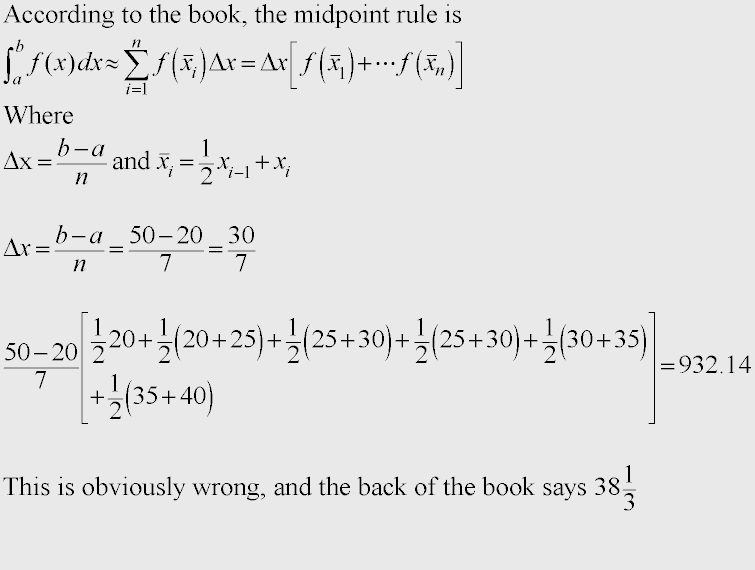SUMMARY
The discussion focuses on estimating the average value of a continuous function f on the interval [20, 50] using the Midpoint Rule. Participants clarify the correct setup for the midpoint formula, emphasizing that delta x should be calculated as (b - a)/n, resulting in (50 - 20)/6. The midpoint sum is computed using the function values at the midpoints, leading to an average value of approximately 38.3333 after dividing by the interval length of 30. The correct application of the formula is crucial for accurate results.
PREREQUISITES
- Understanding of the Midpoint Rule in numerical integration
- Familiarity with calculating averages of functions
- Basic knowledge of continuous functions and their properties
- Ability to perform arithmetic operations with fractions and decimals
NEXT STEPS
- Study the derivation and application of the Midpoint Rule in numerical analysis
- Learn about other numerical integration techniques such as Trapezoidal Rule and Simpson's Rule
- Explore the concept of Riemann sums and their relation to integrals
- Practice calculating average values of functions over different intervals
USEFUL FOR
Students in calculus, mathematicians, and anyone interested in numerical methods for estimating integrals and averages of continuous functions.