Estimating the Gradient of a Graph: Student's Attempt

[chwala]

Homework Statement

Draw the tangent to the curve at the point where $x=1$. Use this tangent to claculate an estimate to the gradient of $y=2^x$ when $x=1$

Relevant Equations

gradient

Ok this is a question that i am currently marking...the sketch is here;

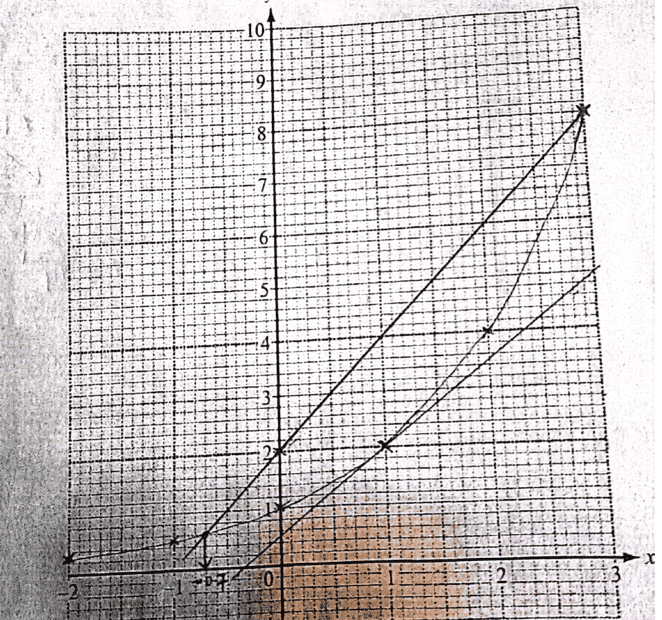
In my mark scheme i have points $(1,2)$ and $(3,5)$ which can be easily picked from the graph to realize an estimate of $m=1.5$ where $m$ is the gradient ...of course i have given a range i.e $1.6≥m≥1.2$

Now to my question. hmmmmm

A student picked the points $(1,2)$ and $(0.9,1.8)$ getting $m=2$ ...the difference from actual is quite big...but the points are picked from their straight line...am i missing something here...

Actual gradient using differentiation would be given by;

$\dfrac{dy}{dx}= 2^x\ln 2$

$\dfrac{dy}{dx}[x=1]= 2^1\ln 2=1.386$

Your insight welcome.

 

[pasmith]

Is the tangent line drawn by the student, or is it printed on the paper?

In any case, I think $(0.9, 1.8)$ is visibly below the tangent line in the picture.

 

[chwala]

Is the tangent line drawn by the student, or is it printed on the paper?

In any case, I think $(0.9, 1.8)$ is visibly below the tangent line in the picture.

Drawn by the student...we would not expect the students to draw this accurately 100%. How do i deal with this? should i increase range of expected values? my thinking is; i cannot penalise the student for having picking those points from their tangent line...and the calculation as per their picked points is correct.

 

[pasmith]

I dont think (0.9, 1.8) is on their tangent line: it's visibly below it. That should result in some loss of marks. If they'd gone with (0.9, 1.85) then they might have a better case.

 

[chwala]

I just checked the accurate graph on desmos...points $(0.9,1.85)$ would have been fine...

 

[chwala]

I dont think (0.9, 1.8) is on their tangent line: it's visibly below it. That should result in some loss of marks. If they'd gone with (0.9, 1.85) then they might have a better case.

Thanks...i agree...i will emphasis the need to try and pick obvious points on the graphs to mitigate this. Cheers great weekend mate!

 

[BvU]

An additional comment: as a physicist, I would emphasize the large error introduced by picking such a small $\Delta x$: any error in $\Delta y$ as read off from the graph is multiplied by 10 !

$\$

 

[WWGD]

Notice in general, unless your function is itself linear to start with, the approximation is only local. But if youre just given the point (1,2), there are infinitely-many lines that go through it. The point (0.9, 1.8) defines just one of infinitely-many such lines. Not sure if this addresses your question.

 

[chwala]

Notice in general, unless your function is itself linear to start with, the approximation is only local. But if youre just given the point (1,2), there are infinitely-many lines that go through it. The point (0.9, 1.8) defines just one of infinitely-many such lines. Not sure if this addresses your question.

Not sure ...we need points that are on the tangent line and as discussed above, it's clear that $(0.9,1.8)$ is not a point on the tangent line to the given curve $y=2^x$.

 

[WWGD]

Not sure ...we need points that are on the tangent line and as discussed above, it's clear that $(0.9,1.8)$ is not a point on the tangent line to the given curve $y=2^x$.

Do you mean at the point (1,2)?

 

[chwala]

Do you mean at the point (1,2)?

Yes.

 

[WWGD]

Yes.

Well, the points (1,2) and (0.9, 1.8) defines the line y2=2x, which contrasts with the line
y1-1=1.386(x-2).
Maybe a bound/estimate for |y1-y2| would help explain why the choice of (0.9, 1.8) was not as good. Additionally , comparing it with the choice of {(1,2),(3,5)} which would define the line y3-2=2(x-1).

Maybe we can find a generic value for
|y-y1|, for y=mx+b.
Hope I'm not too far of.