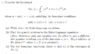CMJ96
- 50
- 0
Homework Statement
Homework Equations
$$f_u- \frac{d}{dx} \left(f_{u'} \right) = 0 $$
$$f_v- \frac{d}{dx} \left(f_{v'} \right) = 0 $$
The Attempt at a Solution
So I calculated the following, if someone could check what I've done it would be greatly appreciated, but I'm not convinced this is right

$$f=(u')^2+2uv+(v')^2$$
$$f_u=2v$$
$$f_v=2u$$
$$f_{u'}=2u'$$
$$f_{v'}=2v'$$
Subbing these into the Euler-Lagrange equations I got
$$v-u''=0$$
$$u-v''=0$$
Then I subbed ##v=u''## into ##u-v''=0## to get ##u-u''''=0##.
Using ##u=e^{\alpha x}## I got the following expression (not sure if this bit is right)
$$u(x)=Ae^{-x} +Be^{x} +Ce^{ix} +De^{-ix} $$
I'm not sure if I can use the boundary conditions to find the extremals with this? it doesn't look like it would simplify down to a tidy solution?