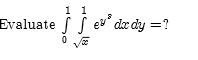Evaluate some kind of gamma function
- Context: MHB
- Thread starter ozgunozgur
- Start date
-
- Tags
- Function Gamma Gamma function
Click For Summary
SUMMARY
The discussion centers on evaluating the gamma function through two integrals: $\int_0^1\int_{\sqrt{x}}^1e^{y^y} dxdy$ and $\int_0^1\int_{\sqrt{x}}^1e^{y^3} dydx$. The first integral is deemed nonsensical due to the lower bound being a function of x, leading to a result that retains x. In contrast, the second integral is simplified by changing the order of integration, resulting in $\int_0^1 y^2e^{y^3}dy$, which is significantly easier to compute.
PREREQUISITES- Understanding of double integrals in calculus
- Familiarity with changing the order of integration
- Knowledge of exponential functions and their properties
- Basic concepts of gamma functions and their applications
- Study techniques for changing the order of integration in double integrals
- Learn about the properties and applications of gamma functions
- Explore integration techniques for exponential functions
- Practice solving complex double integrals with varying limits
Mathematicians, calculus students, and anyone interested in advanced integration techniques and gamma function applications.
Similar threads
Undergrad
Closed Form for Complex Gamma Function
- · Replies 1 ·
- · Replies 3 ·
- · Replies 9 ·
Undergrad
Special Functions: Complete Answers?
- · Replies 1 ·
- · Replies 17 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 3 ·
- · Replies 3 ·
- · Replies 6 ·