Exact constraint in practice -- Pinned joint with 2 DOF

[jasc15]

I've come across this design issue several times, and don't know of any solution in industry. The basic assembly is this:

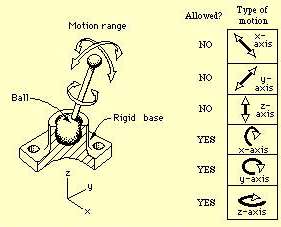
A spherical bearing is fitted to a threaded rod end with a nut to clamp the ball to the rod end. The design intent is to allow angular displacement about the two axes perpendicular to the rod axis (X and Y in the figure), but to constrain rotation about the axis parallel to the rod axis (Z in the figure), as well as constrain translation in all three linear axes. Essentially the constraint provided by a gimbal assembly, or an automotive CV joint, but in a more compact and lower parts-count unit. A splined ball also comes to mind.

In the past, we have simply restrained rotation about the rod axis by fixing a part to the rod with a tab which is bolted to the spherical ball bearing housing. However, the compliance I am seeking requires this tab to twist and bend, which is not ideal.

More simply, referring to the figure, I want the following types of motion allowed:

NO
NO
NO
YES
YES
NO

Thanks.

 

[jambaugh]

From my physics background I consider the symmetry of the coupling in question. The ball has full 3-rotation symmetry. The problem is that rotations about the x and y axes do not commute. Their commutator will be a component of z-rotation. (You can see this on google Earth by rotating the planet by moving your mouse around in a circle on the screen... seriously try it now.)

You're not going to get the two degree of freedom constraint from two moving parts alone. With two parts you either have the 1 axis rotation group, the 3 axis rotation group or one of these plus a translation (via a slider).

So you will need a minimum of 3 parts, A rotating 1-dimensionally w.r.t. B and B rotating 1 dimensionally w.r.t. C to get the type of constraint you're looking for. Hence a classic universal joint or more the more clunky three boards connected by two hinges.

You can attempt some more clever 3 part or more assemblies but you won't reduce things below 3 moving parts.

In a more generic setting the group of transformations between a pair of parts is the Euclidean group. 6 degrees of freedom, 3 rotations and 3 translations. Any constraint on this group will yield a subgroup.
\mathbf{E}^3 = SO(3)\ltimes T^3
Note that rotations will also rotate the direction of translation but in the mechanics setting we can decouple these and consider. The only non-trivial proper (Lie) subgroup of the 3-rotation group are the 1 parameter $SO(2)$ rotating in a given plane, and then, or course translations in only 2, in 1 or in no directions.

You thereby see you basic connectors.

• A free object (relative to a second object we consider "fixed" for the moment) has the full 6 degrees of freedom.
• A ball in a slot maintains the 3 rotation degrees of freedom (DOF) but constrained to only 1 translational DOF.
• A hinge in a slot (or headed bolt in a slot) reduces to 1 rotation and maintains 1 translation DOF.
• A ball in socket keeps 3 rotation DOFs but constrains all translation.
• A fixed hinge or bearing allows only 1 rotation DOF.
• A keyed slot allows only 1 translational DOF.
• You can get 2 translational degrees of freedom (limited) with an additional 1 rotational DOF by using a sliding plate. (Weld two plates together with a spacer and cut a large hole in them. Place a smaller plate between them and weld a rod to it at a right angle through the large hole. Grease it up well and the plate can slide in 2 directions until the rod hits the side of the hole, and the plate can be rotated about the axis of the (perpendicular) rod.) Basically this is $\mathbf{E}^2$ the group of Euclidian motion in the 2 plane.

There may be one or two other mechanisms that allow 2 translational degrees of freedom that escape my imagination but I can't think of any that do not add to the number of parts. But with more than 2 parts you can independently constrain any translational degree of freedom as well as construct more complex curved constraints.

 

[Mech_Engineer]

How about a machined groove (or multiple grooves) in the ball parallel to the Z-axis? Then all you need are matching features in the socket and you've constrained rotation about Z, but still have two rotational degrees of freedom about X and Y.

 

[jasc15]

jambaugh, thanks for your thorough response, though the math is beyond my understanding. It seems to be a generalization of the equations used to find if a structure is statically determinate or indeterminate and to determine the number of degrees of freedom given number of members and number of joints.

Mech_Engineer, that's what I meant when I referred to a splined ball, or a CV joint. More directly though, I am looking for some already-engineered product that I can use, or perhaps some assembly of a minimum number of pre-engineered products. Our area of expertise is engineering the thing being mounted, not the mount itself, so it wouldn't be effective to spend our engineering resources reinventing a wheel that may already exist.

 

[RNickl]

A universal joint would do the job?

 

[Mech_Engineer]

A universal joint would do the job?

I agree, a mounted u-joint would be a good option for this as well. U-joints are also relatively easy to implement in many sizes.