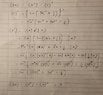SUMMARY
The discussion focuses on calculating the expected value of the variance of energy in coherent states using the non-hermitian and non-commutative raising and lowering operators, denoted as ##a^\dagger## and ##a##. The user expresses uncertainty about their calculations involving the Hamiltonian operators, specifically 2 and . The community emphasizes the importance of the commutation relation between these operators, which is crucial for simplifying the expression ##\langle \alpha | (a^{\dagger} a)^2|\alpha \rangle## to ##|\alpha^*\alpha|^2 \langle \alpha | \alpha \rangle##.
PREREQUISITES
- Understanding of coherent states in quantum mechanics
- Familiarity with raising and lowering operators (##a## and ##a^\dagger##)
- Knowledge of commutation relations in quantum mechanics
- Basic proficiency in calculating expected values in quantum states
NEXT STEPS
- Study the properties of coherent states in quantum optics
- Learn about the implications of non-hermitian operators in quantum mechanics
- Explore the derivation of the commutation relation [##a, a^\dagger##] = 1
- Investigate advanced techniques for calculating expected values in quantum systems
USEFUL FOR
Quantum physicists, students studying quantum mechanics, and researchers focusing on coherent states and operator algebra in quantum theory.