Experiments to distinguish 3-body and 2-body decays?

[unscientific]

I was wondering are there any experiments to distinguish between 2 and 3-body decays? For example, consider decay of the muon and the pion:

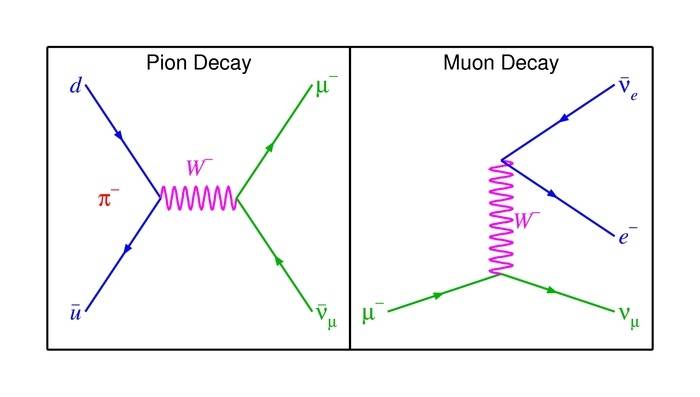
The pion only emits 1 muon neutrino ("missing energy") and 1 muon. The muon however, emits 1 muon neutrino, 1 electron neutrino and 1 electron.

How is it established experimentally that the pion only emits 1 neutrino whereas the muon emits 2 neutrinos?

 

[mfb]

Well, there are experiments to see the neutrinos, but you can measure the energy spectrum of the visible decay product: a two.body decay produces all muons at the same energy (in the pion rest frame), in a three-body decay you get a continuous energy spectrum.

 

[ChrisVer]

In the rest frame of the pion the muon will carry an energy of $E_\mu=\dfrac{m_\pi}{2}$.
In the same result for the muon the electron will have to carry less energy...

 

[ChrisVer]

there are experiments to see the neutrinos,

^ also that ^_^ however I don't know whether there are experiments actually going on with muon decays...

 

[unscientific]

Well, there are experiments to see the neutrinos, but you can measure the energy spectrum of the visible decay product: a two.body decay produces all muons at the same energy (in the pion rest frame), in a three-body decay you get a continuous energy spectrum.

Why is it that in a 2 body decay all muons are produced at the same energy? Since $E_{cm} = E_\nu + E_\mu$, shouldn't there be a spectrum as well?

 

[ChrisVer]

In the rest frame of the pion you initially have a four-momentum:

$P_{in} = \begin{pmatrix} m_\pi \\ \vec{0} \end{pmatrix}~~,~~P_{fin}= \begin{pmatrix} E_\mu + E_\nu \\ \vec{p}_\mu + \vec{p}_\nu \end{pmatrix}~~,~~ E_\nu = \sqrt{|p_\nu|^2 + m_\nu^2} \approx |p_\nu|$

conservation of momentum tells you that:
$\vec{p}_\nu = -\vec{p}_\mu \Rightarrow E_\nu = |\vec{p}_\mu|$

So you have:
$P_{fin}= \begin{pmatrix} E_\mu + |\vec{p}_\mu| \\ \vec{0} \end{pmatrix}$

Take the square equality (I am not sure whether my equations are correct BUT by the fact that I already wrote that $\vec{p}_\nu = - \vec{p}_\mu$ you should already get your answer- in particular they should be fixed numbers for the given decay since you can only have 1 variable):
$E_\mu^2 + |p_\mu|^2 + 2 E_\mu |p_\mu| = m_\pi^2$
$2 |p_\mu|^2 + 2E_\mu |p_\mu| = m_\pi^2 - m_\mu^2$
$\sqrt{m_\mu^2 + |p_\mu|^2}= \dfrac{ m_\pi^2 - m_\mu^2}{2|p_\mu|}- |p_\mu|$
$m_\mu^2 + |p_\mu|^2 = \Big( \dfrac{ m_\pi^2 - m_\mu^2}{2|p_\mu|}\Big)^2+ |p_\mu|^2- (m_\pi^2 - m_\mu^2)$
$m_\mu^2 +(m_\pi^2 - m_\mu^2)= \dfrac{ (m_\pi^2 - m_\mu^2)^2}{4|p_\mu|^2}$

$|p_\mu|= \frac{1}{2} \sqrt{\dfrac{ (m_\pi^2 - m_\mu^2)^2}{m_\mu^2 +(m_\pi^2 - m_\mu^2)}}$
which is a fixed number and so is the muon energy...
Forget my m_pi/2 that would be the case for equally massive produced particles.

 

[ChrisVer]

In a 3 body decay $1 \rightarrow 2+3+4$ the condition for momentum conservation in the rest frame of 1 would be:
$\vec{p}_2= - \vec{p}_3 - \vec{p}_4$
Which doesn't give a fixed number anymore , you can change 3 and 4 freely to keep the equality. In particular if I say that $\vec{p}_3,\vec{p}_4$ are such to give the equality right, then $\vec{p}_3^\prime= \vec{p}_3 +\vec{a}$ and $\vec{p}_4^\prime= \vec{p}_4 - \vec{a}$ can still keep the equality. This gives an ambiguity in the momenta and so the energies which results in a continuous spectrum.

That is a general fact difference between 2 and 3 body decays, and it was the reason why neutrinos were first demonstrated.

 

[mfb]

That is a general fact difference between 2 and 3 body decays, and it was the reason why neutrinos were first demonstrated.

Good point.

Another way to see the difference:
2-body decay: let the x-direction be along the motion of one particle, the other will then move in negative x direction. You get two unknowns (the momenta of the two particle), and two conservation laws - energy and momentum. The result is a single solution.
3-body decay: suddenly you get 1+2+2 unknowns (you have to take the second dimension into account), and only 3 conservation laws (energy, and momentum in two dimensions). That leaves two degrees of freedom for the decay mechanism.