SUMMARY
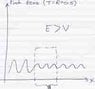
The discussion centers on the tunneling paradox in quantum mechanics, specifically regarding a quantum particle encountering a potential barrier of height V_0 and width a. Participants clarify that for a 50% chance of reflection and transmission, both reflected and transmitted waves maintain the same amplitude, which is 1/{\sqrt {2}} of the incident wave. When the particle's energy is less than the barrier height, the wave inside the barrier becomes an "evanescent wave," decaying exponentially, while outside it oscillates. The probability density is derived from the wave function by multiplying it by its complex conjugate.
PREREQUISITES
- Understanding of quantum mechanics principles, particularly wave-particle duality.
- Familiarity with potential barriers and tunneling phenomena.
- Knowledge of wave functions and probability densities in quantum mechanics.
- Basic grasp of complex numbers and their conjugates in mathematical contexts.
NEXT STEPS
- Study Griffiths' "Quantum Mechanics" for a deeper understanding of wave functions and tunneling.
- Learn about the mathematical derivation of probability densities from wave functions.
- Explore the concept of evanescent waves and their implications in quantum mechanics.
- Research the implications of potential barriers in quantum tunneling experiments.
USEFUL FOR
Students of quantum mechanics, physicists exploring tunneling phenomena, and educators seeking to clarify concepts related to wave functions and probability densities.