Here is my (decidedly naive) take on the situation. I have put it in a spoiler, because I feel you should NOT look at it unless you are totally stumped.
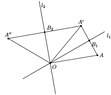
[sp]Suppose we have two non-parallel lines $l_1$ and $l_2$. Call the point they intersect at, $O$.
Call the angle between the two lines (going counter-clockwise), $\theta$. We're going to need some more names, later, I'll introduce the cast of characters as we go along.
Now suppose we have a point, $P$. For the moment, we'll assume $OP$ is at some angle $\phi$ clockwise from $l_1$.
Let's track what happens to $P$, as we reflect first about $l_1$, and then about $l_2$.
Call the point $P$ gets reflected to, $P'$. At this point, the line $OP'$ is at an angle of $2\phi$ with the line $OP$.
Now the line $OP'$ is at some angle $\psi$ (clockwise) from $l_2$. Let's assume (for visualization purposes) that $\phi < \theta$, so that $OP'$ lies between $l_1$ and $l_2$ (you can consider the "other cases" later, on your own).
When we reflect about $l_2$, the point $P'$ gets sent to a new point, let's call it $Q$. As you can readily verify (do this!), the line $OQ$ makes an angle of $\psi$ (counter-clockwise) with $l_2$.
Now when $OP'$ got reflected, the angle between $OP'$ and $OQ$ is clearly $2\psi$. So what angle is $OQ$ from $OP$?
The total angle is: $2\phi + 2\psi$. But $\phi + \psi = \theta$, so the total angle is $2\theta$.
In other words, the angle between $OP$ and $OQ$ doesn't depend on $\phi$, only $\theta$.
Now, one reflection "makes the plane mirrored" (changes the orientation of things). The second reflection "cancels that", so our orientation is preserved, leaving only a change in angle (a rotation).
To get an idea of the "other cases", let's suppose $P$ is "between" $l_1$ and $l_2$. So now $OP$ is at an angle $\phi$ counter-clockwise from $l_1$. So when we reflect, it goes "backwards" -by an angle of $-2\phi$.
Now $OP'$ makes an angle of $\theta + \phi$ with $l_2$. Since we were calling this angle $\psi$, we have:
$\psi = \theta + \phi$, or: $\theta = \psi - \phi$.
When we reflect about $l_2$, the line $OQ$ makes an angle of $2\psi$ with $OP'$. What angle is this line to $OP$?
Well, our original line $OP$ was already $\phi$ towards $l_2$ out of $\theta$. So the original angle between $OP$ and $l_2$ was $\theta - \phi$.
Now, we are $\psi$ "past" $l_2$, so $OQ$ is at an angle of:
$\psi + \theta - \phi = \theta + (\psi - \phi) = \theta + \theta = 2\theta$
with $OP$. Amazing!
Since reflections are isometries, and isometries are, by definition, "distance-preserving", it should be clear that the lengths of the line segments $OP$ and $OQ$ are equal.
It should be suggestive, then, that our two reflections are equivalent to a rotation about the point $O$, with angle equal to twice the angle between $l_1$, and $l_2$.
This is not what I would consider a "proof", but merely a suggestion as to what one is trying TO prove.
Note this only considers the case where $l_1$ and $l_2$ intersect. They might not intersect, or (even more interestingly!) they might be THE SAME line. What do you suppose happens in these two cases?[/sp]
Being more algebraically-minded than a geometer, I would be inclined to write an isometry in THIS form:
$T(x,y) = A\begin{bmatrix}x\\y \end{bmatrix} + \begin{bmatrix}a\\b \end{bmatrix}$
Where $A$ is a 2x2 matrix with $\det(A) = \pm 1$,
because when I calculate something, I like to have some numbers to work with. Of course, to make this work, you need a "formula" for the line you are reflecting about, so you can determine the matrix $A$ and the "translation vector" $(a,b)^T$.
If that formula was, for example:
$l_1: y = mx + b$
I would first translate by $(0,-b)$ to create a "new line" $l_1'$ that goes through the origin, rotate that line so it lies on the $x$-axis, reflect about the $x$-axis, rotate back, and then translate by $(0,b)$.
While this may seem a bit computationally complex, it has the advantage of being able to say PRECISELY what the result of $T(x,y)$ is, for any point $(x,y)$.