Explaining Orientation of Oriented Manifold

[AKG]

The main problem I have with this question is just the wording:

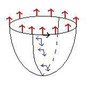
If M is an oriented manifold by means of the restriction of the form dx \wedge dy, describe explicitly the induced orientation on \partial M -- i.e. clockwise or counterclockwise in the plane z = 1.

I don't understand the underlined part. Perhaps it means that the orientation for each (x, y) \in M, \mu _{(x, y)} is the one such that dx \wedge dy (x, y) is the volume element of M_{(x, y)} determined by the standard inner product and orientation \mu _{(x, y)}. Am I interpreting it correctly, or am I reading much more into what's actually said there, and if it's the latter, what is the correct interpretation? Thanks.

 

[HallsofIvy]

Yes, that's what it means.

 

[mathwonk]

yes i agree. you cannot restrict an orientation to a lower dimensional manifold, but you can restrict it to one of the same dimension. so dx^dy can be restricted to a 2 manifold.


then there is for the same reason no unique way to restrict an orientation to a boundary. you have to say how to treat the outward normal vector.



so you usually say something like; if v is a basis for the tangent space to the boundary M, and w is an outward normal vector, then we require (v,w) is an oriented basis for M. or you could say that (w,v) is an oriented basis for M. whatever.

once you decide it determines the orientation of the boundary.

but without knowing which convention they chose , i cannot answer the question you stated.

i do have some lengthy notes on the matter.

 

[mathwonk]

excerpt:
Induced orientation on a boundary.
Next we will show how to induce an orientation on ∆X, whenever X is oriented. It will follow in particular that the boundary of an orientable manifold is also orientable. This will give another proof that every sphere is orientable, since a sphere is the boundary of an orientable closed ball.

Assume for a moment the following result.
Lemma: If V in W is a subspace of a finite dimensional space, then orientations for any two of the spaces V,W, W/V, determines a unique orientation for the third space such that if B is a basis for V, and (A,B) is any extension to a basis for W, and hence å determines a basis A' for W/V, then sign(A')sign(B) = sign(A,B).
I.e. if we have assigned +1 to every basis in one equivalence class and -1 to every basis in the other equivalence class in two of these spaces, this equation tells how to assign these symbols to bases of the other space.

How to assign the boundary orientation
Let X be an oriented (n+1) manifold with boundary. At every boundary point p there is a unique outward unit normal vector np. At each such point p, np represents a basis vector of the normal space TpX/Tp∆X, which thus determines an orientation of that space. Now we can determine an orientation of Tp(∆X) as follows. A basis {v1,...,vn} is positively oriented if and only if the basis {n,v1,...,vn} is a positively oriented basis for TpX.
We claim this determines an orientation for ∆X.

 

[AKG]

Sorry, this was part b) to another question. Yes, M is a 2-dimensional manifold, it is the manifold {(x, y, z) in R³ : x² + y² = z < 1}, where the boundary is just the unit circle in the plane z=1 centered on the z-axis.

I've attached a picture of what I think is going on. The blue things are orientations on the "main part" of the manifold, and the red arrows are the outward pointing unit normals. The black arrow is the arrow for the boundary point that would have to be chosen in order for it and the red arrow together to have the same orientation as it would otherwise have. Is this right?

 

[AKG]

Suppose x \in \partial M, and \mu (and hence \mu _x) is given. Then if \{(e_1)_x\} is a basis of (\partial M) _x and n(x) \in M_x is the outward pointing normal vector at x, then if [n(x), (e_1)_x] = \mu _x, then [(e_1)_x] = (\partial \mu )_x is the induced orientation. I need to find if (e_1)_x points clockwise or counterclockwise given \mu (and hence each \mu _x).

Since M is oriented, \mu is conistent, so if I find that the orientation at some boundary point is clockwise, then it is clockwise for all points on the boundary. For each x \in M, there can be one of two orientations \mu _x, so I think what I need to do is say that if (for x on the boundary now) \mu _x = [(v_1)_x,\, (v_2)_x], then we're looking at the induced orientation at the boundary being counterclockwise, and if \mu _x = -[(v_1)_x, \, (v_2)_x], then the induced orientation is clockwise, right? So instead of one answer, I have to show how the answer depends on \mu _x. Isn't this as simple as saying:

If \mu _x = [n(x), v_x] where v_x is clockwise, then the induced orientation is clockwise, and otherwise the induced orientation is counterclockwise? Do I need to do anything with dx \wedge dy? Oh, wait. I know that:

(dx \wedge dy)(x)(n(x), v_x) &gt; 0

And I have to compute this to see whether the v that will satisfy this inequality (ensure that the left side is greater than 0) is clockwise or counterclockwise.

(dx \wedge dy)(x)(n(x), v_x) &gt; 0

(dx(x) \wedge dy(x))(n(x), v_x) &gt; 0

(dx(x)n(x))(dy(x)v_x) - (dx(x)v_x)(dy(x)n(x)) &gt; 0

n_1v_2 - v_1n_2 &gt; 0

v_2 &gt; v_1\left (\frac{n_2}{n_1}\right )

I should be able to find n(x) separately, and this will give me v_x = (v_1, v_2, v_3)_x. I think I would then think of placing the vector v with it's tail at x, and see whether it points clockwise along the unit circle in the z=1 plane, or counterclockwise. Is this the right approach?