- #1
gkirkland
- 11
- 0
Can someone please explain the below proof in more detail?

The part in particular which is confusing me is
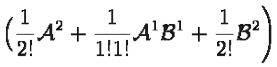
Thanks in advance!
The part in particular which is confusing me is
Thanks in advance!
gkirkland said:Can someone please explain the below proof in more detail?

The part in particular which is confusing me is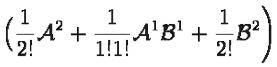
Thanks in advance!
Well, the technical term is "distribute," but yes. Sometimes math is silly like that, though, so I wouldn't be too irritated that you didn't see it.gkirkland said:Oh ok! So they show the first two terms and "FOIL" it out for simplicity sake. I've been staring at this thing for 20 minutes and can't believe I didn't realize that.
That was a great explanation, thanks!
(A+B)^2=A^2+AB+BA+B^2gkirkland said:Could you also explain the 1/2!(AB+BA) portion in the last line?
gkirkland said:Won't you end up with differing coefficients even with further expansion?
such as [tex]\frac{1}{4}S^2T^2 - \frac{1}{2}S^2T^2[/tex]
Strictly speaking, you can only do step 2 as you wrote it if ##A## is diagonalizable. For instance, in the case where you getgkirkland said:For example, if I'm given a matrix A and asked to find the exponential of A these are the steps I take:
1) Find eigenvalues and then eigenvectors of A
2) Form a matrix P consisting of eigenvectors of A
That is ##B=P^{-1}AP##, and see my comment above.gkirkland said:3) Find a matrix B such that [tex]B=PAP^{-1}[/tex]
These steps are actually inverted. Once you have ##B=P^{-1}AP##, using the Taylor expansion you get directly thatgkirkland said:4) Match B to a known form
5) Then [tex]e^{At}=Pe^{Bt}P^{-1}[/tex]
Again, be careful that since [itex]B=P^{-1}AP[/itex], you get [itex]e^A=Pe^BP^{-1}[/itex] (note the order of ##P## and ##P^{-1}##).gkirkland said:Ok, so check my logic on this one:
If you can form a matrix [itex]P[/itex] (ie: [itex]A[/itex] is an [itex]n x n[/itex] matrix and has [itex]n[/itex] eigenvalues with [itex]n[/itex] independent eigenvectors) [itex]B=P^{-1}AP[/itex] will form a diagonolized matrix and then [itex]e^A=P^{-1}e^BP[/itex] so you reach a solution fairly easily.
In one of your posts, your notes readgkirkland said:If A is an [itex]n x n[/itex] matrix and has [itex]n[/itex] eigenvalues and less than [itex]n[/itex] independent eigenvectors then [itex]P[/itex] won't form a diagonalized matrix and you must match [itex]A[/itex] to a known form of [itex]B[/itex]?
I'm still hazy on what to do when you can't form a diagonalized matrix [tex]P[/tex]
so I guess that the answer to that is shown earlier.As shown earlier, an invertible 2x2 matrix ##P## [...] such that the matrix ##B## has one of the following forms
That one is actually diagonalizable. But if you change the -1 to 1, you get a single eigenvector ##( 1\ 0)^T##, and you construct ##P## using ##(0\ 1)^T## as the second vector, such thatgkirkland said:As an example, how would you solve the matrix [itex]\begin{matrix} 1 & 2 \\ 0 & -1 \end{matrix}[/itex] as I believe it only has 1 independent eigenvector.
Use itex instead of tex.gkirkland said:Sorry for the format, I don't know how to do tex code inline
An exponential operator is a mathematical symbol that represents repeated multiplication of a number by itself. It is denoted by the symbol "^", and is read as "to the power of". For example, 2^3 means 2 multiplied by itself 3 times, or 2 x 2 x 2, which equals 8.
The proof for the exponential operator is based on the fundamental properties of exponents, which state that when multiplying numbers with the same base, you can add their exponents. For example, 2^3 x 2^4 can be simplified to 2^(3+4), which equals 2^7. This proof can be extended to any number of terms, showing that the exponential operator follows the same rules as traditional exponentiation.
The exponential operator is useful in simplifying and solving complex mathematical expressions, especially those involving repeated multiplication. It also plays a key role in many scientific and engineering applications, such as in the fields of physics, chemistry, and computer science.
The exponential operator and the caret symbol are often used interchangeably, but they can have different meanings depending on the context. In mathematics, the caret symbol is typically used to represent both exponentiation and bitwise XOR operations, while the exponential operator specifically represents exponentiation.
Yes, the exponential operator can also be applied to non-numeric values, such as variables, functions, and matrices. In these cases, the operator represents repeated multiplication or multiplication of a function or matrix by itself, similar to how it works with numeric values.