Exploring Level Curves of a Function with Maple

[Yankel]

Hello all,

I am trying to draw the level curves of this function:

\[z=\frac{x^{2}+y^{2}}{y}\]

at C=-1,-2,1,2

I started with C=1, and I got kind of stuck with this shape

\[x^{2}+y^{2}=y\]

Maple gave this as the answer, I don't get it:

View attachment 1879

thanks !

 

[Ackbach]

Maple is definitely not giving you a good picture. These level curves are all of them circles. Different $z$ values have the effect of raising and lowering the circles. I'm not terribly familiar with Maple, but plotting these functions is often a matter of using some sort of implicit plot, since your function is defined implicitly. Sage gave me circles as a plot, which confirms what I think they ought to be. Check Maple's documentation and see if there isn't a specific command for plotting implicit functions.

\begin{align*}
zy&=x^{2}+y^{2} \\
0&=x^{2}+y^{2}-zy \\
\frac{z^{2}}{4} &=x^{2}+y^{2}-zy+ \frac{z^{2}}{4} \\
\frac{z^{2}}{4} &= x^{2}+ \left( y- \frac{z}{2} \right)^{ \! 2}.
\end{align*}
This is the equation of a circle centered at $(0,z/2)$ of radius $z/2$.

 

[HallsofIvy]

Don't expect Google to do your thinking for you! Your picture looks funny for two reasons: 1) The curves are not closing on the x-axis and, 2) your x and y-axes have different scales: the distance from 0 to 1 on the x-axis is larger than the distance from 0 to 1 on the y-axis so the circles look like ellipses. In any case, whoever gave you this problem expects you to be able to complete the square as Ackbach did.

 

[chisigma]

Almost ever the use of polar coordinates conducts to a more simple solution... in this case we obtain... $\displaystyle \frac{x^{2} + y^{2}}{y} = a \implies r = a\ \sin \theta\ (1)$

... where $\theta$ must produce a value of $r \ge 0$...

Kind regards $\chi$ $\sigma$

 

[alphy]

Hello there,

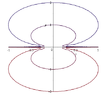
It's great that you are using Maple to explore level curves of a function. Level curves are a useful tool for visualizing the behavior of a function in two dimensions. In this case, the function you are exploring is \[z=\frac{x^{2}+y^{2}}{y}\] and you are interested in the level curves at different values of C, specifically C=-1,-2,1,2.

When C=1, the level curve is given by the equation \[x^{2}+y^{2}=y\] This is a circle with center at (0,1/2) and radius 1/2. It may seem confusing at first because the equation is in terms of x and y, but remember that the level curve represents all points (x,y) where the function has the same value of C=1. Therefore, every point on this circle has the same value of z=1.

As you change the value of C, the shape of the level curve will change accordingly. For example, when C=-1, the level curve will be a circle with center at (0,-1/2) and radius 1/2. When C=2, the level curve will be a circle with center at (0,2) and radius 1.

I hope this explanation helps you better understand the shape of the level curves for this function. Keep exploring and experimenting with different values of C to see how the level curves change. Maple is a great tool for visualizing mathematical concepts and I encourage you to continue using it in your research. Best of luck!