Exponential Functions Problem, find k and a in f(x)=ka^(−x)

[Yankel]

Hello all,

I am trying to solve the following problem:

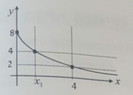
In the given graph, we see the function:

\[f(x)=ka^{-x} , x\geq 0\]

View attachment 8053

1) Find k and a

2) Find x1

3) Show that an increase of 2 units in x brings a 50% reduction in the value of the function f.

I have tried solving it, but taking two known points from the graph and putting them in the function. I got immediately that:

\[k=8\]

and than less clear, that:

\[a=-\sqrt{2}\]

In the matter of fact, I got two solutions, a solution without the minus sign was there too, but it didn't match the given points...so in order to solve (2), I just guessed and checked my guess.

I am not sure how to show number (3).

Can you kindly verify that my solution is correct and assist with section 3 ? What am I missing with the multiple solutions for a ?

Thank you in advance !

 

[Greg]

Hi Yankel.

1) $k=8$ is correct. To find $a$, solve $8a^{-4}=2$ for $a$. Can you continue? (Hint: Choose the positive root.)

2) Solve $8a^{-x_1}=4$ for $x_1$. Okay?

3) We'll complete this after the two exercises above. :)

 

[Yankel]

Hi,

If I am not mistaken a is equal to the square root of 2.

Then x1 is 2. Correct ?

 

[Greg]

That's correct. :)

 

[Yankel]

So...how do we continue with number 3 then ? :-)

I took the function we get, put x+2 instead of x and divided the value of f with x by the value of f with x+2. Got 2. Is if sufficient ?

 

[Greg]

Certainly is. Good work! :D