kyphysics
- 685
- 445
I'm trying to clarify my terminological understanding of things related to mathematical expressions.
Actually, first I want to make sure I understand what an expression is and is not.
From my current understanding, an expression is any number, variable, or combination of numbers and variables linked together by addition or subtraction.
Examples:
4 + 3
4x +3
1/3x^2 - 14x + 2y
The components of an expression are:
terms, factors, constants, and coefficients
Terms are the values linked by +/-. Factors are the things being multiplied (e.g., 4 and x in the second example above). Constants are numbers (like the 3 in first and second example). And coefficients are the numbers in front of variables (like 4 and 1/3 in the second and third example above. Am I right about this so far?
Also, in the third example, the second term is 14x. Would we say it's 14x or -14x. Similarly, would we say the coefficient is 14 or -14?
Questions:
What are monomials, binomials, and polynomials? Are they simply types of expressions?
On the "Math Is Fun" website, they state:
I'm slightly confused.
1.) So, polynomials can't have variables in the denominator, but they can have a denominator?
2.) Also, they can't have negative exponents, but they can have exponents?
3.) I've seen on a YouTube video a person saying that monomials, binomials, trinomials, etc. are ALL polynomials, because "poly" means many and doesn't specify the number of terms. So, technically, according to this YouTube video maker, monomials are also polynomials. Is this true?
Just trying to nail down my terminology!
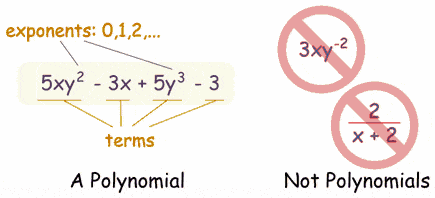
The above image was taken from: https://www.mathsisfun.com/algebra/definitions.html
Actually, first I want to make sure I understand what an expression is and is not.
From my current understanding, an expression is any number, variable, or combination of numbers and variables linked together by addition or subtraction.
Examples:
4 + 3
4x +3
1/3x^2 - 14x + 2y
The components of an expression are:
terms, factors, constants, and coefficients
Terms are the values linked by +/-. Factors are the things being multiplied (e.g., 4 and x in the second example above). Constants are numbers (like the 3 in first and second example). And coefficients are the numbers in front of variables (like 4 and 1/3 in the second and third example above. Am I right about this so far?
Also, in the third example, the second term is 14x. Would we say it's 14x or -14x. Similarly, would we say the coefficient is 14 or -14?
Questions:
What are monomials, binomials, and polynomials? Are they simply types of expressions?
On the "Math Is Fun" website, they state:
A polynomial can have constants, variables and the exponents 0,1,2,3,...But it never has division by a variable.
I'm slightly confused.
1.) So, polynomials can't have variables in the denominator, but they can have a denominator?
2.) Also, they can't have negative exponents, but they can have exponents?
3.) I've seen on a YouTube video a person saying that monomials, binomials, trinomials, etc. are ALL polynomials, because "poly" means many and doesn't specify the number of terms. So, technically, according to this YouTube video maker, monomials are also polynomials. Is this true?
Just trying to nail down my terminology!
The above image was taken from: https://www.mathsisfun.com/algebra/definitions.html