Factorising High order polynomials

  • Thread starter Thread starter MMCS
  • Start date Start date
  • Tags Tags
    Polynomials
Click For Summary
SUMMARY

The discussion centers on factorizing high-order polynomials, specifically one with coefficients 1, 2, 4, and 8. The user seeks guidance on the factorization process and mentions having identified roots as (s+2)(s^2+4), although they are unsure how to arrive at this conclusion. Participants emphasize the importance of correctly identifying roots and suggest that the user should be aware of special polynomial forms that may appear in exams. The conversation highlights the need for clarity in posting questions to receive effective assistance.

PREREQUISITES
  • Understanding of polynomial equations and their properties
  • Familiarity with factorization techniques for polynomials
  • Knowledge of identifying roots of polynomials
  • Basic algebra skills, including manipulation of algebraic expressions
NEXT STEPS
  • Research the Rational Root Theorem for identifying potential roots of polynomials
  • Learn about synthetic division and its application in polynomial factorization
  • Explore special polynomial forms such as quadratic and cubic polynomials
  • Study techniques for solving higher-order polynomial equations, including numerical methods
USEFUL FOR

Students preparing for mathematics exams, educators teaching polynomial factorization, and anyone interested in improving their algebraic problem-solving skills.

MMCS
Messages
151
Reaction score
0
Find roots of:

upload_2015-4-18_14-49-48.png


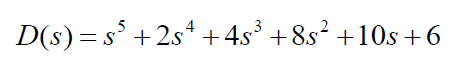
I need to set =0 then factorise. I know that this polynomial has coefficients of 1,2,4,8 and there is a rule to factorise this however, i don't know it.

Also, i believe a high order polynomial will be included in my exams. Are there any other "special" polynomials such as this which i should look out for to make factorizing easier as it has been suggested a polynomial such as this will come up...

Thanks

ADDED: i should add, this is not a homework question. I have the roots to be (s+2)(s^2+4)...but forgot to note how to arrive at this
 
Last edited:
Physics news on Phys.org
MMCS said:
Find roots of:

View attachment 82187

I need to set =0 then factorise. I know that this polynomial has coefficients of 1,2,4,8 and there is a rule to factorise this however, i don't know it.

Also, i believe a high order polynomial will be included in my exams. Are there any other "special" polynomials such as this which i should look out for to make factorizing easier as it has been suggested a polynomial such as this will come up...

Thanks

ADDED: i should add, this is not a homework question. I have the roots to be (s+2)(s^2+4)...but forgot to note how to arrive at this
Your polynomial can't have (s + 2) has a factor, otherwise D(-2) would be zero, which it isn't. If the partial factorization you show is correct, then there's a typo in the polynomial whose image you attached. Otherwise, I don't know how you could get the factorization you show.

Also, when you post a question in the homework section, please use the homework template.
 
MMCS said:
Find roots of:

View attachment 82187

I need to set =0 then factorise. I know that this polynomial has coefficients of 1,2,4,8 and there is a rule to factorise this however, i don't know it.

What happened to 10 and 6? These are coefficients as well.

Also, i believe a high order polynomial will be included in my exams. Are there any other "special" polynomials such as this which i should look out for to make factorizing easier as it has been suggested a polynomial such as this will come up...

Thanks

ADDED: i should add, this is not a homework question. I have the roots to be (s+2)(s^2+4)...but forgot to note how to arrive at this

If this is not a Homework question, then post it in the General Math forum.
 
Well its work. I am doing it at home. Your issue is pedantic.
 
Mark44...the fact that the roots are incorrect is irrelevant. My question is clearly asking how to treat a polynomial of this structure. Your response is therefore uselss
 
MMCS said:
Well its work. I am doing it at home. Your issue is pedantic.
No, it's not.

By posting here in the Homework forums, which are intended to be used by students for their course work, there is only so much help which can be offered, according to the Rules of PF. No solutions of any kind can be given directly to the poster.

In the technical forums, these restrictions are relaxed, and this results in a very different kind of interaction between poster and those interested in replying.
 
MMCS said:
Mark44...the fact that the roots are incorrect is irrelevant.
How is this fact irrelevant? You post a problem, and say that you got a certain factorization, but that factorization is incorrect. Most people who post here would think that was relavant (and even valuable) information.
MMCS said:
My question is clearly asking how to treat a polynomial of this structure. Your response is therefore uselss
How about losing that attitude? You clearly came here for help, and to dismiss any help with such a snippy arrogant tone makes me less interested in providing that help, or even saying what I did to arrive at my answer. We are all unpaid volunteers here - we do it because we like to help out.
 
  • Like
Likes   Reactions: gracy
This is the 4th comment posted in this thread without any sort of constructive answer. Two "mentors" have jumped straight onto this thread with two separate issues. It seems "mentors" on this site or more concerned with rules and regulations than helping people. Mark44 posted problem here is clear and concise, so to go out of your way to ask me to use the template without any sort of help with the actual problem is wasting both of our time.
 

Similar threads

Factoring polynomials-Can there be fractions?
  • · Replies 6 ·
Replies
6
Views
3K
Undergrad Quintic Polynomial Tschirnhaus Transform: Possible complex Bring Radicals
  • · Replies 0 ·
Replies
0
Views
2K
Using binomial coefficients to find sum of roots
  • · Replies 3 ·
Replies
3
Views
2K
Factoring polynomial - Seems difficult
  • · Replies 9 ·
Replies
9
Views
5K
Finding values for a and b for this polynomial
  • · Replies 8 ·
Replies
8
Views
3K
Create a polynomial with desired characteristics, factoring
  • · Replies 3 ·
Replies
3
Views
2K
Factoring a four term polynomial
  • · Replies 11 ·
Replies
11
Views
3K
Confusion about definition of a splitting field
  • · Replies 1 ·
Replies
1
Views
2K
Complex roots of a quartic polynomial
  • · Replies 7 ·
Replies
7
Views
4K
How can I factor a 3rd order polynomial using the cubic formula?
  • · Replies 5 ·
Replies
5
Views
3K