Falling EM system contradicts the equivalence principle?

[jcap]

The following is an improved version of my previous post https://www.physicsforums.com/threa...contradicts-the-equivalence-principle.964594/

Consider the following system comprising a particle on the left with charge $+q$ that is a large distance $d$ away from two oppositely charged particles on the right, with charges $+q$,$-q$, held apart by a spring of length $L$ and spring constant $k$.

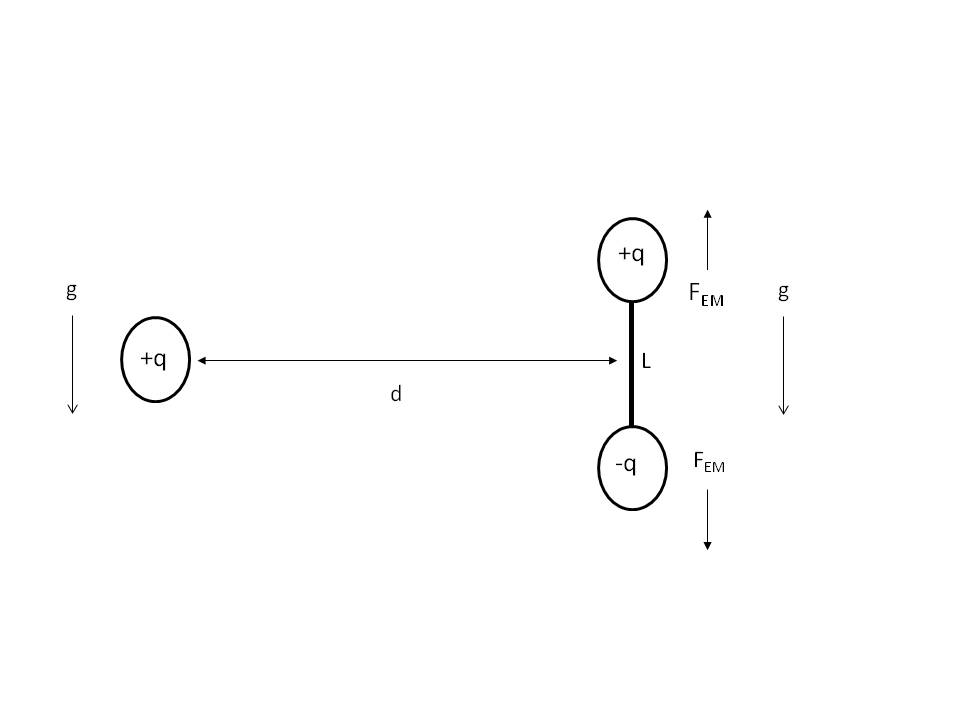
Let us assume that the left-hand particle is sufficiently far from the right-hand particles so that the "static" horizontal component of the electric field that it produces near those particles is negligible. (Actually this assumption is not necessary. We could have another charge $+q$ on the other side of the vertical dipole connected to the first by a horizontal rod. They could then be as close as we like as the horizontal electrostatic forces that they produce on the dipole will cancel out.)

To start with consider the system at rest in empty space. The only electric forces acting on the right-hand particles are "static" attractive forces that are balanced by the compressed spring.

Now let us assume that the whole system is falling in a gravitational field with acceleration $g$. According to the equivalence principle this situation should be indistinguishable from the system in empty space.

But now as the left-hand charge $+q$ has an acceleration $g$ it should produce a "radiative" vertical component to the electric field in the vicinity of the right-hand particles.

Each right-hand particle is subjected to an extra vertical electromagnetic force whose magnitude is given by

$$F_{EM}=\frac{q^2}{4\pi\epsilon_0 d c^2}g.$$

As the forces on the differently-charged right-hand particles point in opposite directions, the spring is stretched by an amount given by

$$\Delta L=\frac{2F_{EM}}{k}.$$

Thus a local observer can tell that he is falling in a gravitational field which contradicts the equivalence principle.

What's gone wrong?

 

[Nugatory]

But now as the left-hand charge $q$ has an acceleration $g$

As do the the spring and the two right-hand particles... so you are trying to analyze the behavior of the system using the non-inertial frame in which an object at rest experiences a proper acceleration of $g$ and an object subject to no forces accelerates in violation of Newton's second law. You can do the problem that way if you want, but it is somewhat non-trivial - far easier to work in the inertial frame in which all three particles are at rest and you can use Maxwell's laws as they are usually written.

But if you do want to do this problem the hard way, you cannot

assume that the left-hand particle is sufficiently far from the right-hand particles so that the "static" horizontal component of the electric field that it produces near those particles is negligible.

This assumption is equivalent to saying that terms in $1/d$ are negligible, but the apparent discrepancy you've found is itself a $1/d$ term. You can't ignore the $1/d$ electrostatic term but include the $1/d$ magnetic term and expect to get a consistent result.

(Actually this assumption is not necessary. We could have another charge +q+q on the other side of the vertical dipole connected to the first by a horizontal rod. They could then be as close as we like as the horizontal electrostatic forces that they produce on the dipole will cancel out.)

Right, and in that case you don't have a $1/d$ term that you're declaring negligible, you have a genuine cancellation to zero that will be present in the non-inertial frame as well - it's just that there are magnetic as well as electrostatic components that cancel.

You might want to give thsi wikipedia article a try: https://en.wikipedia.org/wiki/Paradox_of_radiation_of_charged_particles_in_a_gravitational_field

 

[Dale]

But now as the left-hand charge $+q$ has an acceleration $g$ it should produce a "radiative" vertical component to the electric field in the vicinity of the right-hand particles.
...
What's gone wrong?

Why would it radiate? The proper acceleration is still 0.

Of course, in non-inertial frames you can get weird coordinate expressions for the fields, but those are just coordinate expressions and not particularly meaningful. And you would have to be much more specific about the coordinates to calculate those coordinate expressions anyway.

 

[Vanadium 50]

According to the equivalence principle this situation should be indistinguishable from the system in empty space.

That's not what the equivalence principle says.
Can you state the equivalence principle? If not, we should start there instead.

 

[vanhees71]

The equivalence principle is about local objects, the em. field is not. There's a long history about the question, whether a freely falling point charge radiates or not. The answer is that it does radiate and that this does not violate the equivalence principle:

https://doi.org/10.1016/0003-4916(60)90105-6

 

[Dale]

The equivalence principle is about local objects, the em. field is not. There's a long history about the question, whether a freely falling point charge radiates or not. The answer is that it does radiate and that this does not violate the equivalence principle:

https://doi.org/10.1016/0003-4916(60)90105-6

With radiation defined very carefully to account for the different frames

 

[jcap]

Why would it radiate? The proper acceleration is still 0.

Of course, in non-inertial frames you can get weird coordinate expressions for the fields, but those are just coordinate expressions and not particularly meaningful. And you would have to be much more specific about the coordinates to calculate those coordinate expressions anyway.

I agree there's no proper acceleration so i guess the charges don't radiate.

 

[jcap]

That's not what the equivalence principle says.
Can you state the equivalence principle? If not, we should start there instead.

I suppose the statement of the EP that I'm more comfortable with is the idea that the effect of a gravitational field is equivalent to an accelerating reference frame.

 

[Vanadium 50]

And that is not a correct description of the equivalence principle.