SUMMARY
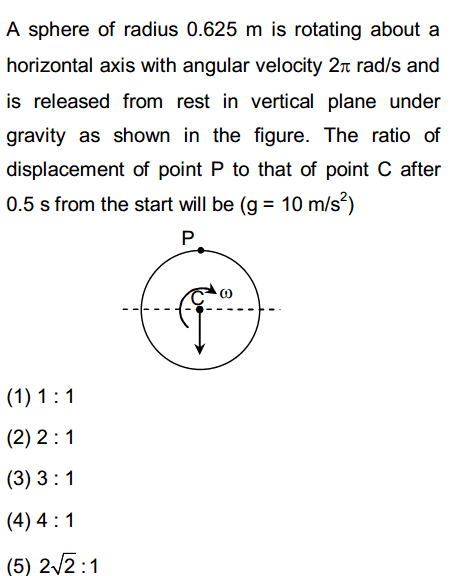
The discussion focuses on calculating the displacements of points P and C on a falling rotating sphere after 0.5 seconds. The solution involves determining the centripetal acceleration and using the equation for free-falling bodies to compute the displacement of point C. For point P, the angle is calculated using the angular velocity, which is given as π radians per second, leading to a displacement of 2r (1.25 m). The final ratio of displacements between points P and C is established as 2:1, accounting for the sphere's rotation.
PREREQUISITES
- Understanding of centripetal acceleration
- Knowledge of angular velocity and its application
- Familiarity with free-fall equations
- Basic principles of rotational motion
NEXT STEPS
- Study the equations of motion for free-falling bodies
- Learn about centripetal acceleration in rotating systems
- Explore angular displacement calculations using angular velocity
- Investigate the effects of rotation on displacement in physics
USEFUL FOR
Students studying physics, particularly those focusing on mechanics, as well as educators and tutors looking to enhance their understanding of rotational motion and displacement calculations.