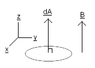Faraday's Law, Magnetic Flux, and the dot product

[apples]

Homework Statement

We are studying Electromagnetic Induction right now. I understand the concepts, Faraday's Law and magnetic flux. But I don't understand what my book is doing.

Homework Equations

Magnetic Flux
\phi=\intB∙dA

Faraday's Law
Emf = - d\phi/dt
Emf=Electromotive force
\phi=Magnetic Flux

And of course the dot product.
x∙y= xy cos\theta

The Attempt at a Solution

I think I shouldn't have written Farday's law here, a bit irrelevant.

Anyway, what the book is doing is confusing me (It is doing this through out the chapter).
When solving for magnetic flux, it says that a wire loop is at right angles to a magnetic field B.
So, according to me, the dot product of the magnetic field and the area of the loop is supposed to be 0, because they are at right angles, and cos 90= 0.

But in the solutions, here is what the book says (Exact words):
"With the field at right angles to the loop, B∙dA = B dA"

In another example it says, "Here the field is uniform and at right angles to the loop, so the flux is just the product of the field with the loop area."

Why? If it's at right angles then it should be 0. cos 90 = 0

 

[Hootenanny]

But in the solutions, here is what the book says (Exact words):
"With the field at right angles to the loop, B∙dA = B dA"

Notice that the area element, dA, is a vector. The area element is a special case of a surface element. Now, the orientation of a surface is usually defined by it's normal vector. So in the case of the wire loop, the surface is perpendicular to the magnetic field vector, but the normal vector of the area element is parallel to the magnetic field. It is this normal vector that defines the direction of dA.

Therefore in this case, dA is parallel to B and hence the dot product is simply B*dA. Do you follow?

 

[Pengwuino]

The dA is the vector area you're integrating over. The area has a direction. In this case, it is along the direction of the magnetic field so B dotted with dA is simply BdA.

 

[bartek2009]

The vector dA = dAn where n is a unit vector normal to the plane of the little element of area dA, this means that if you place your loop in x-y plane, dA will point in the direction of z-axis and so if B is at right angles to the loop which is in x-y plane it also points in the direction of z-axis and is actually parallel to dA making the dot product BdA. (see the picture attached)

----

 

[apples]

Oh cool, I didn't know that the direction of a surface is defined by its normal vector.
Thanks guys. Now it makes sense.