Faraday's Law: Solving Problem w/ Induced Electric Fields

[center o bass]

Homework Statement

A closed metallic square loop with sides with length L is in the xy-plane. The magnetic field varies in the x-direction as B_z = B_0 \sin{\left(\pi x/L\right)}. The loop is being pulled with a constant speed v along the x-direction.

a) Determine the emf in the loop by Faraday's law.
b) Repeat the computation by first calculating the induced electric field in each of the 4 edges of the loop.

Homework Equations

\varepsilon = - \frac{d\phi_B}{dt} = - \frac{d}{dt} \int \vec{B} \cdot \vec{dA} = \oint \vec{E} \cdot \vec{dr}

The Attempt at a Solution

a) This one is okay I think. Since x = vt i have
\varepsilon = A\frac{dB}{dt} = \frac{B_0 A \pi v}{L} \cos (\pi v t /L).

But I don't under stand how to proceed on b). How can I calculate the Efields on the edges and how would this help me? Can anyone help me here?

 

[hikaru1221]

Hmm, this is a weird B-field. Perhaps that's just an approximation.
a/ I don't think that's correct. Remember, dB/dt is not constant, since the loop spreads from x to x+L. You should integrate to obtain magnetic flux through the whole loop first when one edge of the loop is at position x, then differentiate it w.r.t. t. There is also another trick to solve this much faster.
b/ What happens in the reference frame where B-field doesn't varies with time and the wire is moving is that there is Lorentz force exerting on the free electrons and making them move along the wire: F = evxB. This is why exists the induced emf as seen in this reference frame: emf = sigma(EdL) = sigma(F/e) = sigma(vxB). Part b simply asks for computing the emf along each side of the loop, then add them up and compare with the result obtained in part a to show that Faraday's law is consistent with the real phenomenon observed in a particular reference frame.

 

[center o bass]

Why do you say it's weird? :)

Allright I think I got you there. Since B varies of the area of the loop we then have

\int \vec{B} \cdot \vec{dA} = B_0 \int_0^L \int_x^{x+L} \sin{\frac{\pi x}{L}} dx dy = 2B_0L \cos{\frac{\pi x}{L}}

which implies that since dx/dt = v

\left|\frac{d}{dt} \int \vec{B} \cdot \vec{dA}\right| = 2B_0 v\sin{\frac{\pi vt}{L}}

and since the B-field is increasing for x = 0 to x = 0 + epsilon the induced emf must be such that it creates a current that in turn creates a magnetic field that opposes the change in B. This gives

\varepsilon_{ind} = -2B_0 v\sin{\frac{\pi vt}{L}}

Is this one correct? What is the much faster way you are talking about? :)

b) so the reason they are after the E-field is just that \int \vec{E}\cdot \vec{dL} = \epsilon = \frac{1}{q} \int \vec{F} \cdot \vec{dL} = \int \vec{v \times B} \cdot \vec{dL}?

I think I get the right soltion then, the work on the left and on the right side is

LvB_0 \sin{\frac{\pi x}{L}} and LvB_0 \sin{\frac{\pi (x + L)}{L}} = -LvB_0 \sin{\frac{\pi x}{L}}
and since they are opposing each other

\frac{W}{q} = 2B_0 v\sin{\frac{\pi vt}{L}}

Have I got this straight now?

 

[hikaru1221]

I haven't checked the calculation yet, but it seems that you're on the right track

About the "weird B-field", when I first read the question, I, again, imagined of an *infinitely* spread field (see the other topic you opened that I replied) I'm not sure if practically there is a setup to create this kind of B-field, but I guess it's theoretically possible for a B-field to have B_z vary in such way at every points on ONE plane.

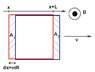
The much faster way is kind of tricky. See the picture. Consider the loop during a time interval dt, it moves from the "red" position to the "blue" one. So the change in magnetic flux is actually just due to the 2 areas A1 and A2 (now you see you don't have to calculate the whole flux through the loop? This is the trick ). We have:
d\Phi = \Phi (A_2) - \Phi (A_1) = B(x+L)\times dx \times L - B(x)\times dx \times L = (B(x+L)-B(x))Lvdt
Now it's easy to deduce induced emf.

But this trick also points out another old but still interesting insight: Because \vec{v} is perpendicular to two parallel sides of the loop, A1 and A2 are actually the areas that those two parallel sides sweep through in dt. That means, the other 2 sides have nothing to do with the change in flux or induced emf! This is consistent with part b. We can see that \Phi (A_1) = B(x)vLdt which corresponds to the work on the 1st side & \Phi (A_2) = B(x+L)Lvdt corresponding to the work of the 2nd side

Now that's the key of Faraday's law. The actual phenomenon is of part b, where the induced E-field is in fact due to Lorentz force. However due to the above fact, this phenomenon can be considered as consistent with Faraday's law, provided that we now consider the area that the loop sweeps through is the cause of the induced emf.

Go a bit more deeply, A1 or A2 actually represents one of the two parallel sides. Now think a little bit: the sides are in the loop, so they are connected, and that leads to the fact that there is induced current. But what if the sides are NOT connected? No current, obviously, since it's open circuit. But even if there is no current, the voltage or emf can still exist. So maybe the induced emfs on two sides have nothing to do with each other! Furthermore, the electrons on one side should NOT know what is happening on the other side. That means, if one side is broken, in the case that electrons can *see and think*, the other side will be affected. But electrons cannot, so the other side is not affected! That, again, leads to the conclusion that the induced emf on each side is independent from the other side.

That means, a moving rod (like a side cut separately from the loop) in this B-field can have induced emf, and experiments show so. So in order to make this phenomenon consistent with Faraday's law, we can consider the swept area of this rod is the "area" of the rod, as we did earlier with A1 and A2. This seems to be some kind of luck, coincidence, or maybe it's just a mathematical fact, isn't it? Maybe, or maybe not. This thought may have some kind of connection with that electromagnetic field is relative, or dependent on the reference frame (what do the electrons "see" in its own reference frame?). But I'll stop here; sorry for digressing too much