Faraday's Law - Spatial Varying Magnetic Field Problem

[scoldham]

Homework Statement

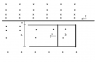
The figure attached shows a rod of length L = 10 cm that is forced to move a a constant speed of v = 5.00 m/sec along horizontal rails. The rod, rails, and connecting strip at the right form a conducting loop. The rod has a resistance of 0.4 \Omega and the rest of the loop has negligible resistance. A current of 100 A through the long straight wire at a distance a = 10.0 mm from the loop sets up a nonuniform magnetic field through the loop.

Find the emf and current induced in the loop.

Note: sorry about the shotty diagram... paint is a cruel mistress... the x's are the B field going into the page and the *'s are coming out of the page... the point is that the field is NOT uniform.

Homework Equations

1. \Phi_B = \int{\vec{B} \bullet d\vec{A}}

2. \epsilon = B l v

3. B = \frac{\mu_0}{2\pi} \frac{I}{r}

4. \epsilon = -\frac{d \Phi_B}{dt}

5. I = \frac{\epsilon}{R}

The Attempt at a Solution

I feel like finding the current is pretty simple once I've managed to calculate the emf by using eqn # 5.

The emf is where I am really struggling. I know that I can calculate the flux (and be able to deduct the emf) using eqn #3 as a function for B. But that requires I know the area of the loop and I'm pretty sure I have insufficient information for that... Equation 2 gives me the B field at a point (again, subing eqn 3 for B) but that doesn't really help me...

I've been looking through my book and the internet for hours.. but I am missing something.. A push in the right direction would be much appreciated...

 

[kuruman]

The emf is where I am really struggling. I know that I can calculate the flux (and be able to deduct the emf) using eqn #3 as a function for B.

Can you show us how to calculate the flux?

But that requires I know the area of the loop and I'm pretty sure I have insufficient information for that... Equation 2 gives me the B field at a point (again, subing eqn 3 for B) but that doesn't really help me...

Maybe you need the area, maybe not. What you really need is an expression for dΦ/dt, the rate of change of flux with respect to time, which brings me back to the original question, how will you calculate the flux? It clearly is not "magnetic field times area" because, as you very correctly pointed out, the field is not uniform over the area of the loop.

 

[scoldham]

The only direct equation in the book is #1 from my first post involving both B and dA which I only have one of... Trying to use some imagination here.. but what about this:

\int \epsilon dt = \Phi_B
\int IR dt = \Phi_B

using I from the long wire... and R from the loop (?) but it really doesn't seem to make since to integrate wrt time...

right direction?

 

[kuruman]

The first equation that you posted is the one to use. Note that the field is variable over the area of the rectangle. Consider a strip at distance r from the wire. It has width dr and length y (y is the distance from the sliding rod to the end of the loop segment that is parallel to it). Can you find the magnetic flux element dΦ through this strip? If yes, then you need to add all such contributions (i.e. integrate) to find the total flux through the rectangle.

 

[scoldham]

I appreciate your help so far...

If I'm understanding correctly,

The B field at distance r from the wire is equal to \frac{\mu_0 I}{2\pi r}

The flux for a horizontal strip in the loop is d \Phi = B y dr = \frac{\mu_0 I}{2\pi r} y dr.

If I integrate over the height of the loop, then I am given the flux, with which, I can calculate the emf... by taking the derivative wrt time?

Am I getting closer?

 

[kuruman]

You are understanding correctly and you are getting closer. Do the integral to find the flux, see what you get and if you can't figure out the next step, post what you have done and you will get another hint.

 

[scoldham]

So when I integrate (using limits from a to L), I get

\Phi = \frac{\mu_0 I y}{2 \pi} \left[ ln(L) - ln(a) \right]

I still do not know what y is really. Can I substitute y = \vec{v} = \frac{dy}{dt}. If I do that... how do I take the dt back out? It kind of seems to throw off what I'm working towards - calculating the flux.

 

[kuruman]

First off the flux should be
<br /> \Phi = \frac{\mu_0 I y}{2 \pi} \left[ ln(L+a) - ln(a) \right]<br />

because the far side is at distance L + a if the rod has length L. You can rewrite this as

<br /> \Phi = \frac{\mu_0 I y}{2 \pi} \left[ ln \right(\frac{L+a}{a} \left) \right]<br />

You have calculated the flux, but that is not what the problem is asking. The problem is asking you to find the induced emf which is the negative time derivative of the flux. What do you get when you take the time derivative of the above expression?

 

[scoldham]

It all makes since now. When I take d/dt of the equation, y becomes dy/dt which is velocity and adding a minus sign to both sides of the equation gives me the emf.

I can get the current using I = \frac{\epsilon}{R}

Thank you SO much!

However, I do still have a question. There were several other parts to this question which I've got worked out for the most part. But one is throwing me off. "What is the magnitude of the force which must be applied to the rod to make it move at a constant speed?"

v doesn't appear to vary in the equation... I first though F = qVB = ItVB then setting F = 0 for no acceleration... but if that tells me anything (IF), all I get is the time when V gets to whatever I assign it to be...

 

[kuruman]

Consider a vector element of length dr in the same direction as the current. It will experience a magnetic force dF = i dr x B where B is the local magnetic field vector generated by the wire. You already know the current, so you can integrate to find the net magnetic force. If the rod is to move at constant velocity, then the net force on the rod must be zero. So with what external force must the rod be pulled to get a net force of zero?

 

[scoldham]

Thanks... I believe this give me just what I needed! The assignment is due shortly so I will work out what I think and hopefully I won't hit any more roadblocks.

Thank you for all of your help.