FEA Boundary conditions for basic helical spring deformation

[robs314]

Hello, I was wondering if anyone can help me with my FEA approach.

I want to check that my boundary conditions for a simple quarter torus (representing a section of a helical spring) are correct. I'm neglecting the helical angle at this stage.

I have fixed one end in all axes, and applied displacements to the other end to represent how a quarter of a coil would deform when the whole spring is compressed.

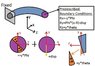
Please see my diagrams, which illustrates my problem clearly, along with my working out. The centre of the spring is at 0,0,0. Displacement is δ, and Phi is ∅.

I think the boundary conditions are not correct, as I am experiencing much higher stresses than I should be.

If anyone out there can help me, it would be of great benefit to me, as I simply do not understand why my assumptions are wrong!

Thanks!

 

[AlephZero]

Presumably if you were doing this right, you would have constant stress along the "length" of the spring, but you got something different.

Personally I wouldn't try to figure this out. I would apply a unit load on the Y direction and let the program work out how much the spring uncoils as it stretches. You could distribute the load over the whole of the end face, if you don't want a stress concentration applying it all at the center of the circle.

 

[robs314]

Many thanks for your response Alephzero

You are correct that my stress values should be constant along the length (arc) of the wire, but are not.

Unfortunately, I think that applying displacements to the boundary is the only way I can get it to deform as it should.

As I am only looking at a section of the coil (rather than the whole coil) I don't think I can apply a force in the y-axis alone. The wire is effectively in torsion, so the force must be going through a point offset from the circle centre for this to occur.

I did try the approach you suggested, and unfortunately it didn't deform as it should.

Thankyou for the suggestion though - I still think I have to work out the displacement transformations; it should be less complex as I am neglecting the helix angle. Do you have any ideas further to this?

Thanks :)

 

[robs314]

Of course, Alephzero, I may have misinterpreted your advice - could you explain your suggested approach a little more? Thankyou

 

[nvn]

robs314: Try applying forces to your quarter torus, instead of displacements. I did not check your calculations carefully, but your displacements are probably wrong. The absence of your helix lead angle is probably OK and probably will not make a big difference, if the lead angle is small. Your fixed end, at x = 0, looks fine; keep it as-is. Try applying a y-direction force, -P, to the centerpoint of the purple circle in your first attached file, and also apply a torsional moment, Mz = R*P, at the centerpoint of your purple circle. See if this gets you close to the expected stress. Afterwards, you can measure the exact displacements, to see if your applied displacements were right or wrong.

 

[AlephZero]

Hmm... I think I over simplfied the loading a bit. This page
http://school.mech.uwa.edu.au/~dwright/DANotes/springs/intro/intro.html#stressStiffness suggests that you need a shear force and a bending moment, so the load on the "cut" through the wire corresponds to the axial load on the end of the complete spring.

Apart from very local effects at the ends, it shouldn't matter too much how you apply the total force and moment to the end of the spring, any more than it matters for a cantilever beam.

The more I think about the displacement constraints on the spring, the more confused I get, but I'm not convinced you should have any rotation of the section. I can't see how that rotation can continue over a large number of complete turns for the whole spring...

 

[robs314]

Again, thank you for your responses :)

I have been trying what you have both suggested. I have also received some more advice recently, which seems to work:

For symmetry, one end of the coil moves up and the other moves down by the same amount. The end planes must rotate by the total vertical displacement divided by the section length.

So, make one end displace by delta/2 in the positive y direction, and the other end displace by delta/2 in the negative y direction (where delta is the compression displacement).

Then, apply a displacement of Beta*y for the z-axis displacement, where Beta=delta/(0.5*pi*R^2), from Beta=delta/2*pi*(R^2)*N, substituting N=0.25.

This keeps the ends of the spring normal to the main (circular) axis of the coil.

So, Alephzero, you were correct to doubt that the rotation continues over the length of the spring. Instead, I'm applying equal+opposite displacements at both ends, so the 'fixed' section will be in the middle of the section.

I was trying your approach, nvn, of applying a shear force and moment to one end, before I received this other advice. It may well work, but I'm going to concentrate on what I know works now! If I have time at the end, I will try the force approach to compare.

So, these are the boundary conditions now:

One end: Rx=0, Ry=delta/2, Rz=beta*y. The other end: Rx=beta*y, Ry=-delta/2, Rz=0.

Thanks an awful lot for your responses, it's nice to know there are people out there who like to help people in an educational capacity!