Fermat & Snell: Solving the Derivation Mystery

[jonjacson]

Hi folks,

I am reading a book on Fermat's principle and I don't understand one step in the mathematical derivation.

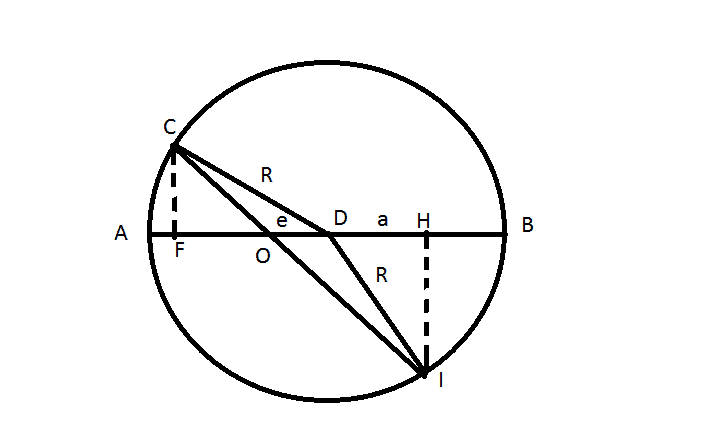
R is the radius of the circle.

C is the source of light that travels to I through two paths COI and CDI.

m is the inverse of the speed in the top medium
n is the inverse of the speed in the lower medium

Using the law of cosines is easy to find CO and OI :

CO² = e² + R² -2 * e * R * cos (eR)

OI² = n² + e² + 2* e * R * cos (eR)

These are distances, we want time, and we can get it by simply multiplying these quantities by the inverse of the speed in every medium.

The book says:

"The time of travel through CDI = m * R + n * R and the time of travel through COI is CO * m + OI * n "

Until here I agree and I see it easy to follow, but then the book says:

"Hence:

m * CO + n * OI = m * R + n * R , to quantities of the first order in e".

I don't see how these two expressions could be equal. For me these are equal only if e is 0 since the equation is saying the time of travel in both paths is the same.

Maybe the key is the sentence "to quantities of the first order in e". Maybe there is a larger expression and they don't show which terms they have neglected.

The book manipulating that expression squaring twice arrives at Snells law.

This paragraph may help to understand this:

"Reverting to Fermat's method of demonstration, we must emphasize again the salient point that he merely restricts himself to proving that the time required for a light ray to traverse a neighbouring virtual path differs from the time actually taken by a quantity of second order. In other words, the variation between the time taken to travel along the actual path and that needed to cover an adjacent virtual path is zero. This condition is necessary but not sufficient for the time to be a minimum".

Do you understand how the left part could be equal to the right part if e is not zero?

 

[robphy]

(Yourgrau's book has some interesting features.)

I think this is the same derivation with different words:
http://www.feynmanlectures.caltech.edu/I_26.html

 

[jonjacson]

(Yourgrau's book has some interesting features.)

I think this is the same derivation with different words:
http://www.feynmanlectures.caltech.edu/I_26.html

That link looks very interesting, thanks!

Yourgrau is the book I was reading but they didn't show explicitly what terms are discarded, I found another book much more comprehensive. It is the book written by Herman Goldstine and its called "
A History of the Calculus of Variations from the 17th through the 19th Century (Studies in the History of Mathematics and Physical Sciences)"

It is a very detailed book that shows you every step on every demonstration.