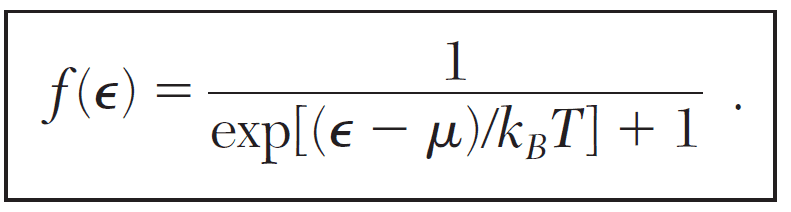SUMMARY
The Fermi-Dirac distribution, denoted as ##f(\epsilon)##, approaches zero as energy ##\epsilon## increases towards infinity at finite temperatures (##T > 0##). At absolute zero (##T = 0##), the distribution is definitively zero for all energy states greater than the Fermi energy (##\epsilon_\mathrm{F}##). This indicates that states above the Fermi energy are unoccupied, confirming that the highest energy state does not possess any particles at absolute zero.
PREREQUISITES
- Understanding of Fermi-Dirac statistics
- Knowledge of Fermi energy (##\epsilon_\mathrm{F}##)
- Familiarity with concepts of absolute zero temperature (##T = 0##)
- Basic principles of statistical mechanics
NEXT STEPS
- Study the implications of Fermi-Dirac distribution in semiconductor physics
- Explore the behavior of particles at absolute zero temperature
- Investigate the differences between Fermi-Dirac and Bose-Einstein distributions
- Learn about the applications of Fermi-Dirac statistics in quantum mechanics
USEFUL FOR
Physicists, students of quantum mechanics, and anyone interested in statistical mechanics and the behavior of particles at various temperatures.