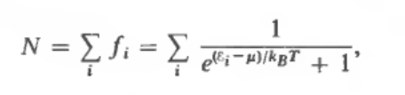matteoargos
- 3
- 1
- TL;DR
- I have I have some doubts about the relationship between the probability of occupying an electronic state defined by the Fermi Dirac distribution and the relationship to the total number N of free electrons in a solid at equilibrium.
Hello
I have some doubts about the relationship between the probability of occupying an electronic state defined by the Fermi Dirac distribution and the relationship to the number N of free electrons in a solid of N atoms.
In particular I refer to the Section 2.2 of Solid State Physics (Ashcroft, Mermin) formula 2.49
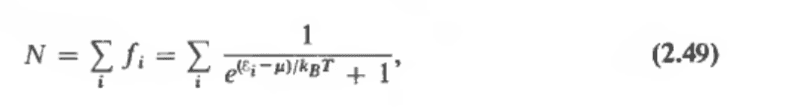
Where: fi is the probability of the one-electron level i being occupied at temperature T in an N-electron system which is the well known Fermi-Dirac distribution

where we neglect the superscript N.
I do not arrive to understand conceptually the 2.49 as N to be summatory of fi contributions. Being f a probability.
In this section is explained that
"fi is the mean number of electrons in the one-electron level"
as proof is indicated that
"[...]A level can contain either 0 or 1 electron (more than one being prohibited by the exclusion principle). The mean number of electros is therefore 1 times the probability of 1 electron plus 0 times the probability of 0 electrons. Thus the mean number of electrons in theleve is numerically equal to the probability of its being occupied. Note that this would not be so if multiple occupation of levels were permitted".
If we think this of course the 2-49 is evident.
Nevertheless I'm used to think to the number of electrons for a certain energy level for a solid like
where g(E) is the density of levels , f(E) is the Fermi distribution
so that N is the integral on the space of the whole E of g(E)f(E)dE (or as the limit of the summatory gi(E) x fi(E) )I miss gi(E) in the first part on the left of the 2.49....
Someone can explain me conceptually this point? Thank you in advance.
I have some doubts about the relationship between the probability of occupying an electronic state defined by the Fermi Dirac distribution and the relationship to the number N of free electrons in a solid of N atoms.
In particular I refer to the Section 2.2 of Solid State Physics (Ashcroft, Mermin) formula 2.49
Where: fi is the probability of the one-electron level i being occupied at temperature T in an N-electron system which is the well known Fermi-Dirac distribution
where we neglect the superscript N.
I do not arrive to understand conceptually the 2.49 as N to be summatory of fi contributions. Being f a probability.
In this section is explained that
"fi is the mean number of electrons in the one-electron level"
as proof is indicated that
"[...]A level can contain either 0 or 1 electron (more than one being prohibited by the exclusion principle). The mean number of electros is therefore 1 times the probability of 1 electron plus 0 times the probability of 0 electrons. Thus the mean number of electrons in theleve is numerically equal to the probability of its being occupied. Note that this would not be so if multiple occupation of levels were permitted".
If we think this of course the 2-49 is evident.
Nevertheless I'm used to think to the number of electrons for a certain energy level for a solid like
n(E)= g(E)f(E)
where g(E) is the density of levels , f(E) is the Fermi distribution
so that N is the integral on the space of the whole E of g(E)f(E)dE (or as the limit of the summatory gi(E) x fi(E) )I miss gi(E) in the first part on the left of the 2.49....
Someone can explain me conceptually this point? Thank you in advance.