- #1
Rudina
- 6
- 7
- Homework Statement
- -If the barbell was dropped from its final height, with what speed (in m/s) did it impact the ground?
- Relevant Equations
- I used the kinematic equation for free fall Vf^2=Vi^2-2g
y. For deltaY I subtracted 88-22.5. I am not sure why I can't get this one right. I might need to use the formula V=gt but I don't know how to get t. Help, please. Thank you
Eddie Hall is the current world record holder in the deadlift, a powerlifting maneuver in which a weighted barbell is lifted from the ground to waist height, then dropped. The figure below shows a side view of the initial and final positions of the deadlift.
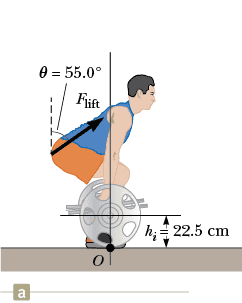
A side view of the initial position of a man performing a deadlift. The man is squatting and leaning forward. A point labeled O is at the lowest point of the circular cross-section of the barbell, which is on the ground, and this point is also located at the bottom of the man's shoe at a distance closer to the front of the shoe than the back of the shoe. A vertical and horizontal line run through the center of the cross section of the barbell and extend through the image. The distance between the ground and the center of the cross-section of the barbell is hi = 22.5 cm. A vector labeled Flift points along the person's back at an angle of 𝜃 = 55.0° from the vertical.
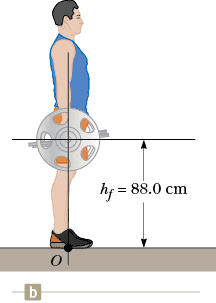
A side view of the final position of a man performing a deadlift. The man is standing straight up. A point labeled O is one the ground at about the midpoint of the man's shoe. A vertical and horizontal line run through the center of the cross section of the barbell and extend through the image. The distance between the ground and the center of the cross-section of the barbell is hf = 88.0 cm.
On March 5, 2016, Hall lifted a combined mass of 465 kg (1,026 lb) from the initial barbell height of 22.5 cm to a height of 88.0 cm above the ground (see figure (b)). As shown in figure (a), the initial lift force for this maneuver is generated by the gluteus maximus parallel to the back of the lifter, at an angle of 55.0° to the vertical.
A side view of the initial position of a man performing a deadlift. The man is squatting and leaning forward. A point labeled O is at the lowest point of the circular cross-section of the barbell, which is on the ground, and this point is also located at the bottom of the man's shoe at a distance closer to the front of the shoe than the back of the shoe. A vertical and horizontal line run through the center of the cross section of the barbell and extend through the image. The distance between the ground and the center of the cross-section of the barbell is hi = 22.5 cm. A vector labeled Flift points along the person's back at an angle of 𝜃 = 55.0° from the vertical.
A side view of the final position of a man performing a deadlift. The man is standing straight up. A point labeled O is one the ground at about the midpoint of the man's shoe. A vertical and horizontal line run through the center of the cross section of the barbell and extend through the image. The distance between the ground and the center of the cross-section of the barbell is hf = 88.0 cm.
On March 5, 2016, Hall lifted a combined mass of 465 kg (1,026 lb) from the initial barbell height of 22.5 cm to a height of 88.0 cm above the ground (see figure (b)). As shown in figure (a), the initial lift force for this maneuver is generated by the gluteus maximus parallel to the back of the lifter, at an angle of 55.0° to the vertical.