Discussion Overview
The discussion revolves around constructing a Venn diagram for three sets A, B, and C, with the conditions that each pair of sets has a non-empty intersection, while the intersection of all three sets is empty. Participants are seeking to verify their proposed diagrams and explore alternative representations.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
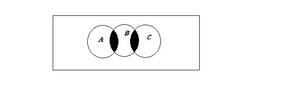
- One participant requests verification of their Venn diagram that meets the specified conditions.
- Another participant points out that the proposed diagram does not satisfy the condition that \(C \cap A \neq \emptyset\).
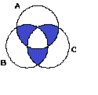
- A suggestion is made to use more complex figures instead of perfect circles for the Venn diagram.
- It is noted that intersections do not have to be represented with shadows only, and objects can be used in the diagram.
- A further response indicates that the proposed diagram fails to meet the condition \(C \cap A = \emptyset\), providing a visual representation of the issue.
Areas of Agreement / Disagreement
Participants do not appear to reach consensus, as there are conflicting interpretations of the conditions and the validity of proposed diagrams. Multiple competing views remain regarding the correct representation of the sets.
Contextual Notes
Some assumptions about the representation of intersections and the use of shapes in Venn diagrams are not explicitly stated, leading to potential misunderstandings in the proposed solutions.