SUMMARY
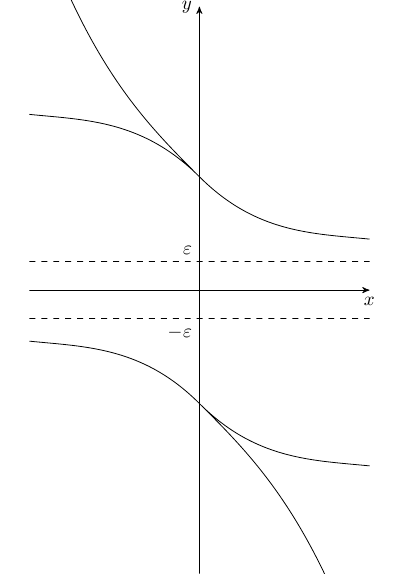
The discussion centers on finding a function $\displaystyle f(x)$ such that $\displaystyle \frac{1}{f(x)}$ is defined for all $\displaystyle x$, is bounded, and $\displaystyle f(x)$ is a decreasing function. It is established that $\displaystyle f(x)$ must not equal zero and must be separated from zero, meaning there exists an $\displaystyle \varepsilon$ such that $\displaystyle |f(x)| > \varepsilon$ for all $\displaystyle x$. A proposed solution is $\displaystyle f(x) = 1 + e^{-x}$, which satisfies the conditions of being decreasing while ensuring $\displaystyle \frac{1}{f(x)}$ is increasing and bounded.
PREREQUISITES
- Understanding of decreasing functions in calculus
- Familiarity with limits and boundedness in mathematical analysis
- Knowledge of exponential functions and their properties
- Basic concepts of function behavior as $\displaystyle x \to \infty$
NEXT STEPS
- Research the properties of decreasing functions and their implications on reciprocal functions
- Explore the behavior of the function $\displaystyle f(x) = 1 + e^{-x}$ in detail
- Study the concept of boundedness in the context of real-valued functions
- Investigate other potential forms of $\displaystyle f(x)$ that meet the specified criteria
USEFUL FOR
Mathematicians, calculus students, and anyone interested in the properties of functions, particularly in the context of boundedness and decreasing behavior.