Find Area of Lemniscate Bounded by Circle: r^2=6sin(2theta) & r=sqrt(3)

[MarkFL]

Here is the question:

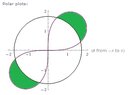
Find the area of the lemniscate...?


Find the area inside the lemniscate r^2=6sin(2theta) and outside the circle r=sqrt(3).

I keep getting 15pi/2, but I am told this is wrong...

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Hello Pete,

First, let's look at a plot of the area to be found:

View attachment 1746

We see that by symmetry, we may double the computation of the first quadrant area to get the total area. First, let's compute the limits of integration by determining at what angles the two curves have intersections in this quadrant:

\(\displaystyle r^2=6\sin(2\theta)=3\)

\(\displaystyle \sin(2\theta)=\frac{1}{2}\)

\(\displaystyle 2\theta=\frac{\pi}{6},\,\frac{5\pi}{6}\)

\(\displaystyle \theta=\frac{\pi}{12},\,\frac{5\pi}{12}\)

Hence the area $A$ is given by:

\(\displaystyle A=2\cdot\frac{1}{2}\int_{\frac{\pi}{12}}^{\frac{5\pi}{12}} 6\sin(2 \theta)-3\,d\theta\)

\(\displaystyle A=3\int_{\frac{\pi}{12}}^{\frac{5\pi}{12}}\sin(2 \theta)\,2\,d\theta-3\int_{\frac{\pi}{12}}^{\frac{5\pi}{12}}\,d\theta\)

On the first integral, we may use the substitution:

\(\displaystyle u=2\theta\,\therefore\,du=2\,d\theta\)

and we have:

\(\displaystyle A=3\int_{\frac{\pi}{6}}^{\frac{5\pi}{6}}\sin(u)\,du-3\int_{\frac{\pi}{12}}^{\frac{5\pi}{12}}\,d\theta\)

Applying the FTOC, we obtain:

\(\displaystyle A=-3\left[\cos(u) \right]_{\frac{\pi}{6}}^{\frac{5\pi}{6}}-3\left[\theta \right]_{\frac{\pi}{12}}^{\frac{5\pi}{12}}\)

\(\displaystyle A=-3\left(-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2} \right)-3\left(\frac{5\pi}{12}-\frac{\pi}{12} \right)\)

\(\displaystyle A=3\sqrt{3}-\pi\)