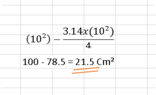Find Area Problem in Multiple Choice Question
- Context: MHB
- Thread starter susanto3311
- Start date
Click For Summary
SUMMARY
The discussion focuses on calculating the area of a shaded region in a geometry problem involving a square and a circle. The square has a side length of 10 cm, resulting in an area of 100 cm², while the circle, with a diameter of 10 cm, has an area of 25π/4 cm², approximately 19.63 cm². The blue shaded area is determined by subtracting the area of the circle from the area of the square, leading to a final result of approximately 21.5 cm². The calculations were confirmed by a participant named Serena.
PREREQUISITES- Understanding of basic geometry concepts, specifically area calculations.
- Familiarity with the formula for the area of a square: A = s².
- Knowledge of the formula for the area of a circle: A = (1/4)πd².
- Ability to perform arithmetic operations involving π (pi).
- Review the properties of geometric shapes, focusing on squares and circles.
- Practice calculating areas of composite shapes involving subtraction of areas.
- Explore the use of π in various mathematical contexts and its approximations.
- Learn about advanced geometry topics, such as area under curves and integration.
Students studying geometry, educators teaching area calculations, and anyone interested in solving mathematical problems involving shapes.
Similar threads
- · Replies 4 ·
- · Replies 11 ·
- · Replies 5 ·
High School
A Simpler Way to Find the Shaded Area?
- · Replies 1 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 2 ·