Find B at Distance r from Capacitor Symmetry Axis

[hastings]

problem:
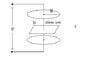
A capacitor has circle plates with radius R. the plates are at a distance h. between the plates there is a tension V. Find B, magnetic induction, at a distance r from the symmetry axis of the capacitor. See diagram attached.

what I did:
I know it has to be studied in two different cases:
1. r<<R
2. r>>R

I know...

(1)V=\int E dl=Eh \longrightarrow E=\frac{V(t)}{h}

(2)\oint E dl=-\frac{d\phi(B)}{dt}

But then how to go on?
Please please please help...!

 

[Gokul43201]

You would do better to use Ampere's law over a circular path centered on the symmetry axis. Then you'll have to use Gauss' Law in each of the two limiting cases.

Start off by writing down the above equation and see how far you can go.