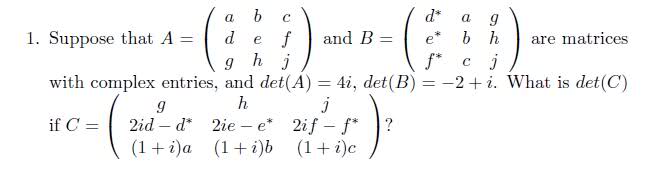SUMMARY
The discussion centers on the properties of determinants, specifically how to find the determinant of matrix C given the determinants of matrices A and B. The key takeaway is that the determinant is a multilinear function of its rows, allowing for the expression of det(A, B+D, C) as det(A, B, C) + det(A, D, C). This property clarifies that while determinants do not simply add when matrices are summed, they can be manipulated through linear combinations of their rows. Understanding this fundamental property is crucial for accurately calculating determinants in linear algebra.
PREREQUISITES
- Understanding of 3x3 matrices and their determinants
- Familiarity with linear combinations of vectors
- Knowledge of multilinear functions in linear algebra
- Basic concepts of matrix operations and properties
NEXT STEPS
- Study the properties of determinants, focusing on multilinearity
- Explore linear combinations of vectors in the context of matrix operations
- Learn about the implications of the determinant in transformations and linear mappings
- Review examples of determinant calculations involving multiple matrices
USEFUL FOR
Students and professionals in mathematics, particularly those studying linear algebra, as well as anyone involved in computational mathematics or engineering requiring determinant calculations.