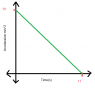
- #1
Govind_Balaji
- 83
- 0
Homework Statement
Find the maximum velocity of the particle using the graph given.(See attachment)
Homework Equations
Initial velocity was not given. I assumed it to be 0.
In book, the solution was 55m/s^2
The Attempt at a Solution
Initial acceleration was ##10m/s^2##. Final acceleration after 11 seconds was ##0m/s^2##.
I figured out that ##a_n=\frac{110-10(n-1)}{11}##, where n is the second and ##a_n## is the acceleration in ##n##th second.
I hope I am right at this step.
I think that velocity will be maximum at 11th second.
So I calculate the velocity at 1st second by
[itex]\begin{align*}v_n&=v_{n-1}+\frac{a_n}{2}\\
&=v_{n-1}+\frac{55-5(n-1)}{11}\\\end{align*}
[/itex].
I derived this using identities of motion and my already derived ##a_n## formula.
[itex]
v_0=0\\
v_1=0+\frac{55-5(1-1)}{11}=5\\
v_2=5+\frac{55-5(2-1)}{11}=\frac{105}{11}\\
...\\
v_{11}=295/11\\
[/itex]
I should get 55m/s.
Please help me out.