Find Mean With Multiple Data [Shortcut]
Click For Summary
SUMMARY
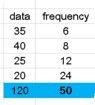
The discussion focuses on calculating the mean of multiple data sets using a shortcut formula. The formula provided is $$\overline{x}=\frac{\sum\limits_{k=1}^n\left(x_kf_k\right)}{\sum\limits_{k=1}^n\left(f_k\right)}$$, which can be implemented in Excel using =SUMPRODUCT(A2:A5, B2:B5) / SUM(B2:B5). Participants clarify that while the formula simplifies the process, it still requires multiplication of each data point by its frequency. The consensus is that this method is the most efficient for calculating the mean from frequency tables.
PREREQUISITES- Understanding of basic statistics, specifically mean calculation.
- Familiarity with frequency tables and their components.
- Basic knowledge of Excel functions, particularly SUMPRODUCT and SUM.
- Ability to interpret mathematical notation and formulas.
- Research the application of frequency tables in statistical analysis.
- Learn advanced Excel techniques for statistical calculations.
- Explore alternative methods for calculating mean in different software tools.
- Study the implications of using weighted averages in data analysis.
Statisticians, data analysts, Excel users, and anyone involved in quantitative research who needs to calculate means efficiently from frequency data.
Similar threads
- · Replies 4 ·
- · Replies 14 ·
- · Replies 24 ·
- · Replies 37 ·
- · Replies 5 ·
- · Replies 4 ·
- · Replies 8 ·
- · Replies 5 ·
- · Replies 7 ·
- · Replies 28 ·
![find mean with multiple data [shortcut].png](/data/attachments/291/291421-e8c93287c3cd6f046c7703e2323995bf.jpg?hash=6Mkyh8PNbw)