I Find P(X+Y>1/2) for given joint density function

[Peter_Newman]

Hey everybody,

I have a joint density of the random variables $X$ and $Y$ given and want to find out $P(X+Y>1/2)$.

The joint density is as follows:

$$f_{XY}(x,y) = \begin{cases}\frac{1}{y}, &0<x<y,0<y<1 \\ 0, &else \end{cases}$$

To get a view of this I created a plot:

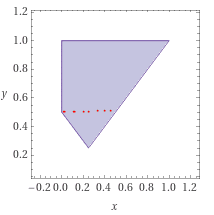
As usual I would split the area up into two sub areas (see red dots) and doube integrate this. In this case for instance my calculation is the following:

$$P(X+Y>1/2) = P(Y>1/2 - X) = \int_{y=0.5}^{1} \int_{x=0}^{y} \frac{1}{y} \, dx dy + \int_{0.25}^{0.5} \int_{x=0.5-y}^{y} \frac{1}{y} \, dx dy \approx 0.5 + 0.1534 \approx 0.6534$$

The solution should be $P(X+Y>1/2) = \frac{\ln(2)}{2}$, which I can not explain, that why I'am asking here. I think in my integral there could be a mistake, but I don't see the error...

I would be very happy for answers to this! Thank you!

 

[andrewkirk]

That looks correct, as far as you've gone.
I suggest you write out the remainder of the steps you took to reach your numeric answer, doing first the inner and then the outer integrals and finally inserting the outer integration limits to obtain a closed formula for the result.
Advisors will then be able to spot any errors in your working.

 

[Peter_Newman]

Hello, thank you for the answer.

I will gladly comply with the request and show here my exact calculation path for the double integral:

$$\int_{y=0.5}^{1} \int_{x=0}^{y} \frac{1}{y} \, dx dy + \int_{0.25}^{0.5} \int_{x=0.5-y}^{y} \frac{1}{y} \, dx dy$$

$$= \int_{0.5}^{1} \left(\int_{0}^{y} \frac{1}{y} \, dx\right) \, dy + \int_{0.25}^{0.5} \left(\int_{x=0.5-y}^{y} \frac{1}{y} \, dx \right) \, dy $$

$$= \int_{0.5}^{1} \left( 1\right) \, dy + \int_{0.25}^{0.5} \left(2-\frac{0.5}{y} \right) \, dy $$
$$= 0.5 + 0.153426$$

But this equals not the "original solution" $P(X+Y>1/2) = \frac{\ln(2)}{2}$...

 

[andrewkirk]

I get 1 - log(2)/2, which is approx 0.653. So my calc agrees with yours. Maybe the book has the wrong answer. It happens.

 

[Peter_Newman]

Hello,

thank you for your reply and confirmation of the calculation. And my integral limits are not set wrong?

I think that assuming there is an error in the book, it comes from the fact that the authors have calculated $P(X+Y<1/2)$, which would be the small triangle that arises when you draw the diagonal to 0. This would be, so to speak, the "white triangle" from the diagonal to the colored area (0 to 0.5 on y-axis and 0.25 x-axis (but integral limits are different here...)...