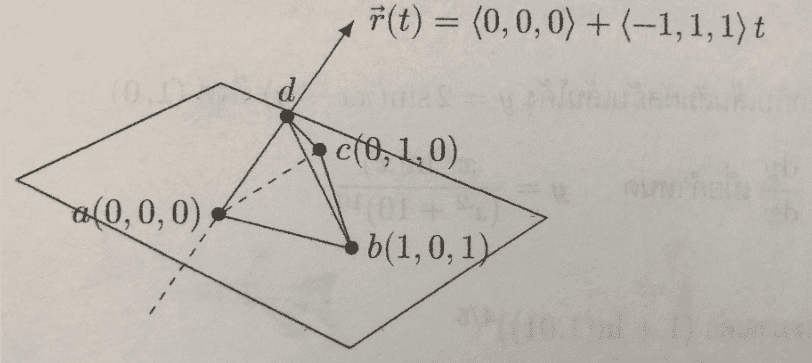SUMMARY
The discussion focuses on determining the coordinates of point D in a triangular pyramid ABCD with a volume of 4 cubic units, where points A(0,0,0), B(1,0,1), and C(0,1,0) lie on the plane defined by the equation -x + z = 0. The area B of the triangular base ABC is calculated as B = 1/2 * ab * ac = 1/2 * √2 * 1. The volume formula V = (1/3)Bh leads to the conclusion that the height h must equal 12√2, resulting in point D being located at coordinates (-12, 12, 12).
PREREQUISITES
- Understanding of three-dimensional geometry and volume calculations
- Familiarity with vector projections and normal vectors
- Knowledge of the equation of a plane in 3D space
- Basic proficiency in solving algebraic equations
NEXT STEPS
- Study the properties of triangular pyramids and their volume calculations
- Learn about vector projections and their applications in geometry
- Explore the derivation and applications of the distance formula from a point to a plane
- Investigate the geometric interpretation of normal vectors in three-dimensional space
USEFUL FOR
Mathematicians, engineering students, and anyone interested in geometric calculations involving three-dimensional shapes and their properties.