MHB Find rs: xy = 1 reflected across y = 2x

[anemone]

Hi MHB,

I recently found an interesting problem which I initially thought I could solve without much trouble, but after I started to work on it, I found out that this has not been the case and this problem has driven me crazy, as I find no good way to attack it...so, I desperately need some help on this problem.

Problem:

The graph $xy=1$ is reflected in $y=2x$ to give the graph of $12x^2+rxy+sy^2+t=0$. Find $rs$.

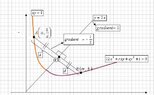
I tried to sketch its graph and here is my sketch:

View attachment 1284

I managed only to get down to finding the relation between $r$ and $s$, i.e. $(3r+s=-33)$, but not the value of the product of them.

Thanks in advance for any help that anyone can offer.

 

[MarkFL]

Re: Find rs

Have you considered that the reflection matrix is:

$$R(m)=\frac{1}{5}\begin{bmatrix}{-3}&{4}\\{4}&{3}\end{bmatrix}$$

 

[anemone]

Re: Find rs

Have you considered that the reflection matrix is:

$$R(m)=\frac{1}{5}\begin{bmatrix}{-3}&{4}\\{4}&{3}\end{bmatrix}$$

Hi MarkFL,

Thanks for the reply but unfortunately, I'm not familiar with matrices...

 

[MarkFL]

Re: Find rs

Okay, what we want to compute, is the product:

$$\frac{1}{5}\begin{bmatrix}{-3}&{4}\\{4}&{3}\end{bmatrix}\begin{bmatrix}{x}\\{y}\end{bmatrix}=\frac{1}{5}\begin{bmatrix}{-3x+4y}\\{4x+3y}\end{bmatrix}$$

And so $xy=1$ becomes:

$$\left(\frac{1}{5}(-3x+4y) \right)\left(\frac{1}{5}(4x+3y) \right)=1$$

Can you proceed from here? (Sun)

 

[anemone]

Re: Find rs

Okay, what we want to compute, is the product:

$$\frac{1}{5}\begin{bmatrix}{-3}&{4}\\{4}&{3}\end{bmatrix}\begin{bmatrix}{x}\\{y}\end{bmatrix}=\frac{1}{5}\begin{bmatrix}{-3x+4y}\\{4x+3y}\end{bmatrix}$$

And so $xy=1$ becomes:

$$\left(\frac{1}{5}(-3x+4y) \right)\left(\frac{1}{5}(4x+3y) \right)=1$$

Can you proceed from here? (Sun)

I'll try my best, hehehe...

If we expand and cross multiply the equation below, we get

$$\left(\frac{1}{5}(-3x+4y) \right)\left(\frac{1}{5}(4x+3y) \right)=1$$

$$(-3x+4y)(4x+3y)=25$$

$$-12x^2-9xy+16xy+12y^2=25$$

$$12x^2-7xy-12y^2+25=0$$

and now, by comparing it with the given equation as follows:

$12x^2+rxy+sy^2+t=0$

We see that $r=-7$ and $s=-12$, and therefore $rs=(-7)(-12)=84$.

But when substituting these values to the equation that relates $r$ and $s$ gives

$3r+s=3(-12)+(-7)=-43\ne -33$, why is that so? Was it because the equation that I found wasn't correct? But...I checked and I'm very certain that I got the right equation of $3r+s=-33$...

 

[MarkFL]

Re: Find rs

I haven't checked your work thoroughly, but one error I see is:

$$\tan\left(\pi-2\tan^{-1}(2) \right)\ne\frac{2}{11}$$

This should be:

$$\tan\left(\pi-2\tan^{-1}(2) \right)=\frac{4}{3}$$

But, this still does not resolve the issue.

 

[anemone]

Re: Find rs

Ops...my bad...I labeled the diagram, the angle between the gradient line of the reflected graph at the intersection point wrongly...

I've uploaded a corrected version of the graph, as shown below:
View attachment 1285
and now, after substituting the values of $r=-7$ and $s=-12$ into the equation

$$\frac{dy}{dx}=\frac{-2r-24}{r+4s}$$

we get

$$\frac{dy}{dx}=\frac{-10}{-55}=\frac{2}{11}$$

but when I tried it with the equation that I simplified, which is $3r+s=-33$, I got $3(-7)+(-12)=-43$...

And I don't know what went wrong with the simplified equation that I obtained...(Angry)

 

[anemone]

Re: Find rs

Okay, what we want to compute, is the product:

$$\frac{1}{5}\begin{bmatrix}{-3}&{4}\\{4}&{3}\end{bmatrix}\begin{bmatrix}{x}\\{y}\end{bmatrix}=\frac{1}{5}\begin{bmatrix}{-3x+4y}\\{4x+3y}\end{bmatrix}$$

And so $xy=1$ becomes:

$$\left(\frac{1}{5}(-3x+4y) \right)\left(\frac{1}{5}(4x+3y) \right)=1$$

Can you proceed from here? (Sun)

Hi MarkFL,

Sorry to bother you again...as I don't know the concept behind all these...would you mind to explain it for me?

Where does the term $$\frac{1}{5}$$ and $$\frac{1}{5}\begin{bmatrix}{-3}&{4}\\{4}&{3}\end{bmatrix}$$ come from?

 

[MarkFL]

Re: Find rs

But $$3(-7)+(-12)=-21-12=-33$$...(Clapping)

 

[MarkFL]

Re: Find rs

Hi MarkFL,

Sorry to bother you again...as I don't know the concept behind all these...would you mind to explain it for me?

Where does the term $$\frac{1}{5}$$ and $$\frac{1}{5}\begin{bmatrix}{-3}&{4}\\{4}&{3}\end{bmatrix}$$ come from?

Here is the article I referenced:

http://www.faculty.sfasu.edu/becneljj/homepage/preprints/reflection.pdf

Look particularly at pages 5 and 6.

 

[anemone]

Re: Find rs

But $$3(-7)+(-12)=-21-12=-33$$...(Clapping)

Argh! I couldn't believe I made such a silly mistake here...and thanks for catching this up for me!

Here is the article I referenced:

http://www.faculty.sfasu.edu/becneljj/homepage/preprints/reflection.pdf

Look particularly at pages 5 and 6.

Hey, thanks for the link! I really appreciate that! And thanks again for the help!Hey MarkFL, yesterday, when I asked you privately if you have any idea on how to tackle this problem, you said you were not interested to it...but now you're the one who replied to me... I hate you! (Tongueout) Now I want you to make some crunchy popcorn and white coffee for me!(Coffee)(Emo)

 

[MarkFL]

Re: Find rs

...
Hey MarkFL, yesterday, when I asked you privately if you have any idea on how to tackle this problem, you said you were not interested to it...but now you're the one who replied to me... I hate you! (Tongueout) Now I want you to make some crunchy popcorn and white coffee for me!(Coffee)(Emo)

Reviewing our conversation, I see that I actually did not reply ( (Tongueout) ) because I was doing other things at that time, and then I quickly forgot about it, until you told me you were going to post it here. So, at that time, having completed my "duties," I began to research the technique of reflections about the line $y=mx$, and found that helpful PDF, from which I was able to figure out what could be done to find the answer to the given problem.

In the end though, I found this problem to be interesting, and I am glad you wound up posting it here because others may benefit from it. So, I will make that popcorn and coffee for you, but I will need you to bring me some refreshing Dew instead for fudging about me saying I was not interested. (Sun)

 

[anemone]

Re: Find rs

Hehehe...alright, I accept your reasoning and I'll bring you the watered down Dew instead...:p(Emo)

 

[MarkFL]

Watered down?!? (Puke) (Swearing) Remind me to keep my eye on you...(Tongueout)

By the way, I suspect there may be another linear equation in $(r,s)$ lurking around in your method.

I am also wondering if there is a more clever technique than either of us is using which gives us the desired product without having to find the factors explicitly...(Thinking)

Fun problem! (Yes)

 

[anemone]

Hey our naughty and playful global moderator, aka MarkFL,

You're right, I found another way to solve for the values for $r$ and $s$ using my method.

My solution:
View attachment 1296

The line $y=2x$ is the perpendicular bisector of the segment AB and this fact leads us to many useful results:

1)

The gradient between the point $A(a, \frac{1}{a})$ and $(1, 2)$ tells us the value for $a$...

$$\frac{2-\frac{1}{a}}{1-a}=-\frac{1}{2}$$ implies $$a=\frac{5-\sqrt{17}}{2}$$.

and

The gradient between the point $B(m, k)$ and $(1, 2)$ tells us the relation between $m$ and $k$...

$$\frac{k-2}{m-1}=-\frac{1}{2}$$ implies $$m=5-2k$$.2)

We see that the curve of $12x^2+rxy+sy^2+t=0$ passes through the intersection point$$\left(\frac{1}{\sqrt{2}},\;\;\frac{2}{\sqrt{2}} \right)$$ between the curve $xy=1$ and the line $y=2x$ and if we merge all these data together with the relation between $r$ and $s$ where $3r+s=-33$, we get

$t=5r+60$

3)

The exact same distance between the point $$A(a, \frac{1}{a})=\left(\frac{5-\sqrt{17}}{2},\; \frac{2}{5-\sqrt{17}} \right)$$, $(1, 2)$ and $B(m, k)=(5-2k, k)$, $(1, 2)$ tells us the value for k...

$$\left(2-\frac{2}{5-\sqrt{17}} \right)^2+\left(1-\frac{5-\sqrt{17}}{2} \right)^2=(k-2)^2+(5-2k-1)^2$$

Solving the equation above we get $$k=\frac{11-\sqrt{17}}{4}$$

At this point, we have all that we need to solve for the value of $r$.

$$12\left(\frac{\sqrt{17}-1}{2} \right)^2+r\left(\frac{\sqrt{17}-1}{2} \right)\left(\frac{11-\sqrt{17}}{4} \right)-(33+3r)\left(\frac{11-\sqrt{17}-1}{4} \right)^2+5r+60=0$$

$r=-7$

$s=-33-3(-7)=-12$

and hence

$rs=(-7)(-12)=84$ and we're done!

 

[Opalg]

I am also wondering if there is a more clever technique than either of us is using which gives us the desired product without having to find the factors explicitly...(Thinking)

I just wanted to add that the condition for the general conic equation $ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0$ to represent a rectangular hyperbola is $a+b=0$. In this case, that tells you immediately that $s = -12$. But I do not see any quick way to find the value of $r$, or to get $rs$ without finding $r$ and $s$ separately.

 

[johng1]

Hi,
Here's my version of reflection about a line:

View attachment 1300

 

[anemone]

Hi,
Here's my version of reflection about a line:

View attachment 1300

Thank you for the note, johng!:)