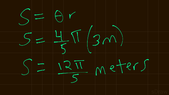Discussion Overview
The discussion revolves around calculating the arc length of a circle, specifically how to convert an angle in radians to a decimal approximation for the arc length. The context includes mathematical reasoning and the use of calculators for conversion.
Discussion Character
- Mathematical reasoning, Homework-related
Main Points Raised
- One participant presents the problem of finding the arc length s with given parameters: an angle of \( \frac{4\pi}{5} \) radians and a radius of 3 meters.
- Another participant notes that the result should be in meters since the radius is given in meters, and suggests using a calculator for decimal approximation.
- A participant inquires about how to use the calculator for conversion, specifically asking about the functionality of their calculator.
- One participant provides a decimal approximation of \( \frac{12\pi}{5} \) as approximately 7.5398.
- Another participant humorously acknowledges the previous calculation by referring to the first participant as their own calculator.
- A participant identifies an error in their calculations, stating they were incorrectly using 180 for pi.
- This participant also provides the unit conversion equation relating degrees to radians.
- One participant expresses gratitude to others for their assistance.
Areas of Agreement / Disagreement
Participants generally agree on the method of using a calculator for conversion, but there is no consensus on the initial calculation process, as one participant identified an error in their approach.
Contextual Notes
Limitations include potential misunderstandings regarding the use of radians and degrees, as well as the specific functionalities of different calculators which may affect the conversion process.