- #1
opus
Gold Member
- 717
- 131
Please see the attached image. It's a part of a study guide for my final, but I didn't put it in the homework section because I already got the answer, I just don't know what it means.
The question has to do with the differential of an arc length. I made some drawings to see if I could make some sense out of it but I don't think I'm quite there.
So when we're talking about the differential of an arc length, what exactly does this mean?
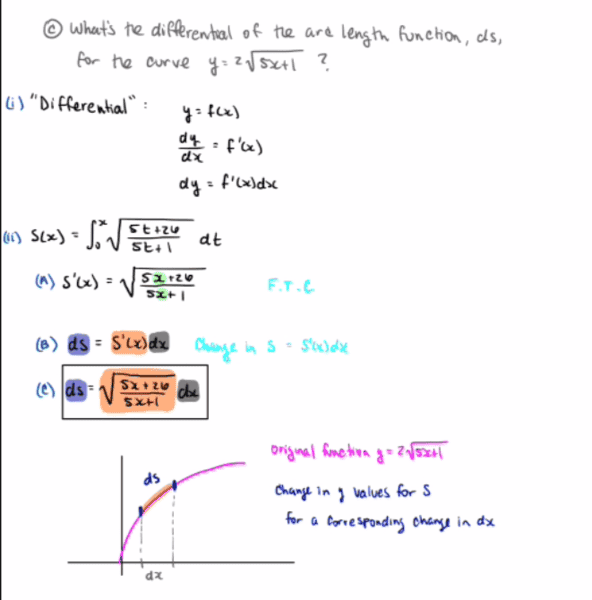
The question has to do with the differential of an arc length. I made some drawings to see if I could make some sense out of it but I don't think I'm quite there.
So when we're talking about the differential of an arc length, what exactly does this mean?

