Find Side AB: Calculate Using m & n Ratios

[quee]

Hello.
There is a problem:
"Through D on a side AB of the triangle ABC drawn a line parallel to AC intersecting BC in E. D is such that CD:DB = m:n. Find DE:AC"

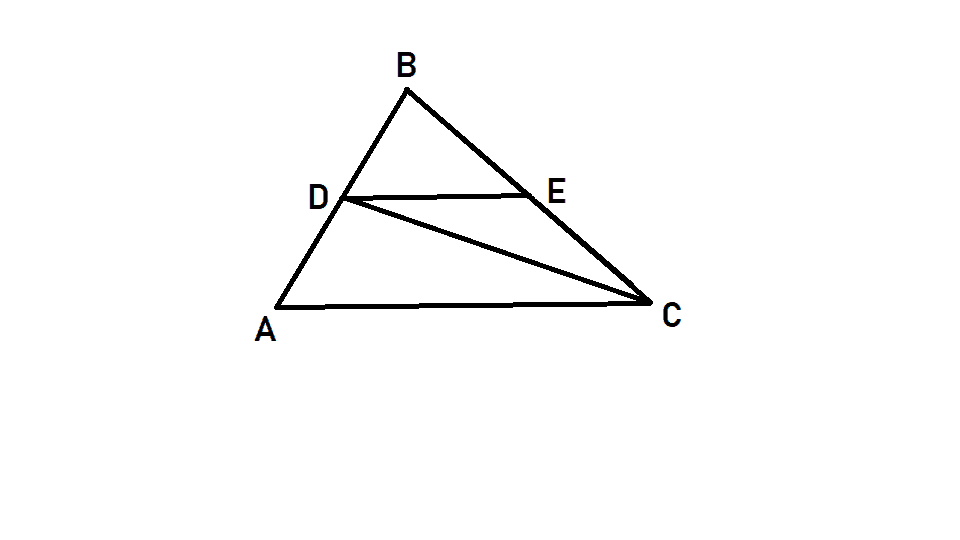
So it is easy to find out that DB:AB equals to DE:AC as DE and AC are parallel. Since DB = n, there is only one need to express AB in terms of n and m. But how to do it? I tried using similar triangles, but I can't get AB through it. The trapezoid ADEC also gives no results as the second diagonal is unknown.

 

[fresh_42]

I think you need also $AE$ and the intersection of both diagonals $AE$ and $CD$ in, say $F$. This will make things more complicated as there will be more lengths involved, but I don't see another way to get hold on $CD$. Then use the intercept theorem.

 

[quee]

I think you need also $AE$ and the intersection of both diagonals $AE$ and $CD$ in, say $F$.

Thank you. Actually, I considered that there may be not enough information in the problem. Now I am convinced.

 

[fresh_42]

Thank you. Actually, I considered that there may be not enough information in the problem. Now I am convinced.

I am not sure. It depends on how the result has to look like. E.g. I got for the quotient
$$\dfrac{DE}{AC} =\dfrac{n}{m} \cdot \dfrac{CD}{AD+DB}$$
but it's not clear whether this will do or not. I don't see a second equation for $CD$.

 

[Antarres]

Since $DE$ is parallel to $AC$, you can use the similarity of triangles $ABC$ and $ADE$. You have from the proportion that is given:
$$AD:DB = m:n \Rightarrow nAD = mDB$$
This means that $AB = AD + DB = \left(\frac{m}{n} + 1\right) DB$. So now you have the proportion between $AB$ and $DB$ and from similarity you get the proportion between $DE$ and $AC$.

 

[SammyS]

Since $DE$ is parallel to $AC$, you can use the similarity of triangles $ABC$ and $ADE$. You have from the proportion that is given:
$$AD:DB = m:n \Rightarrow nAD = mDB$$
This means that $AB = AD + DB = \left(\frac{m}{n} + 1\right) DB$. So now you have the proportion between $AB$ and $DB$ and from similarity you get the proportion between $DE$ and $AC$.

Did you misread the given information?

Statement says: $CD:DB = m:n$, not $AD:DB$.

D is such that CD:DB = m:n. Find DE:AC"

 

[Antarres]

@SammyS Indeed, I completely misread it. Apologies to the OP. In that case the exercise seems more complicated.
Might be that the method fresh gave would work, I so far don't see a clear way to get the proportion.

 

[quee]

Indeed, I completely misread it. Apologies to the OP.

It is okay. Thank you for your reply.
If only $$AD:DB= m:n,$$ it would be completely obvious that $$\frac{DE}{AC} = \frac{n}{n+m}$$
But this is, unfortunately, a much harder problem. Or it may be an actual lack of some information in the problem.