mt91
- 13
- 0
Got a steady state question and was wondering if anyone would be able to check if I'm on the right track?
Find the steady states of these two equations:
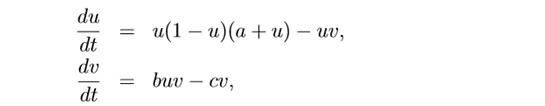
My working out as far:
\[ 0=u*(1-u*)(a+u*)-u*v* \]
\[ 0=v*(bu*-c) \]
I looked at the 2nd equation first giving:
\[ v*=0, u*=c/b \]
subbing v*=0 into equation 1 gave:
\[ 0=u*(1-u*)(a+u*) \]
\[ u*=0, u*=1, u*=-a \]
\[ v=a+c/b - ac/b-c^2/b^2 \]
Not sure about that part of the steady state question so any help would be really helpful, cheers
Giving three steady states of
(0,0), (1,0), (-a,0)
Then I looked at subbing u*=b/c. (However this part of my working got confusing and I'm not entirely sure if it was correct.
\[ 0=c/b(1-c/b)(a+c/b)-cv/b \]
\[ cv/b=c/b-c^2/b^2(a+c/b) \]
Find the steady states of these two equations:
My working out as far:
\[ 0=u*(1-u*)(a+u*)-u*v* \]
\[ 0=v*(bu*-c) \]
I looked at the 2nd equation first giving:
\[ v*=0, u*=c/b \]
subbing v*=0 into equation 1 gave:
\[ 0=u*(1-u*)(a+u*) \]
\[ u*=0, u*=1, u*=-a \]
\[ v=a+c/b - ac/b-c^2/b^2 \]
Not sure about that part of the steady state question so any help would be really helpful, cheers
Giving three steady states of
(0,0), (1,0), (-a,0)
Then I looked at subbing u*=b/c. (However this part of my working got confusing and I'm not entirely sure if it was correct.
\[ 0=c/b(1-c/b)(a+c/b)-cv/b \]
\[ cv/b=c/b-c^2/b^2(a+c/b) \]