How do PI controllers achieve steady state?

[OTSEngineer]

Summary: A question about how PI controllers reach steady state

Hello PhysicsForums,

I need a little help understanding how a PI controller works when operating in steady state.

Here is the equation in State Space form:

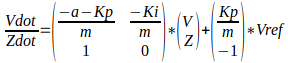
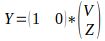
Where

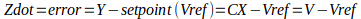
In standard form, the equation is:

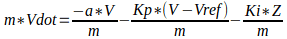
Where

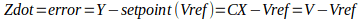The question I’m working on asks for the stead state solution in comparison to both open loop and proportional steady state response. Because (in theory), the integral controller will eliminate all error (assuming no disturbances), all derivatives will equal 0. So, the system should track the setpoint Vref perfectly. I confirmed this by looking the the solutions provided for this question. However, I do not understand mathematically how this is possible unless -a*V is equal and opposite to Ki*Z. I thinking that even if this system had initial conditions where the V=Vref, there must be some deviation from Vref so that the integration of V-Vref over time can have a non-zero value that is equal to -a*V.

Is my conclusion correct?

Thank you.

 

[DaveE]

The integrator "remembers" the history of its inputs, so it doesn't need an error input to maintain the correct output, if it is at the correct output (meaning the output that eliminates the error). It probably does, however, need a historical error in order to settle to the correct output. In fact, in a stable system with constant inputs, the integrator will do what it needs to do to eliminate the error at it's input. This is all for a constant input, of course.

However, your statement that "the system should track the setpoint Vref perfectly" is problematic. Tracking implies changing conditions, which may not be steady state depending on how you are defining that. For example, if Vref is a ramp (i.e. $\frac{dVref}{dt} \neq 0$) then a 1st order integrator can not eliminate the error.

 

[OTSEngineer]

Hello DaveE,
Would you happen to have any documentation on second order integrators in PID controllers?

Thank you for your explanation.

 

[DaveE]

Hello DaveE,
Would you happen to have any documentation on second order integrators in PID controllers?

Thank you for your explanation.

No, at that level it's really just the modern controls textbooks.

There is no second order integrator in PID, by definition. PID isn't really a thing for control systems experts. It's all just Laplace Transforms, Bode plots, and such; the more generic feedback control problem. They would deal more with pole-zero locations as required for their design without the predefined PID format.

There may be documents out there that would help, but I never approached these problems that way.

 

[OTSEngineer]

I suppose then that the modern approach is to develop a transfer function with the poles and zeros needed to insure stability for the anticipated operating conditions. Is that correct?

 

[DaveE]

I suppose then that the modern approach is to develop a transfer function with the poles and zeros needed to insure stability for the anticipated operating conditions. Is that correct?

Yes. Stability and other performance requirements. It might end up being a PID compensation, which is fine, but there's not really a good theoretical reason for predetermining that configuration; for constraining your solution in advance.

 

[OTSEngineer]

Thank you.