Hello Vina,
I am assuming the curve is defined as follows:
$$(x+2y)^2+2x-y-3=0$$
Implicitly differentiating with respect to $x$, we obtain:
$$2(x+2y)(1+2y')+2-y'=0$$
Distribute:
$$2(x+2y)+4(x+2y)y'+2-y'=0$$
Move everything that does not have $y'$ as a factor to the right side:
$$4(x+2y)y'-y'=-\left(2(x+2y)+2 \right)$$
Factor both sides:
$$\left(4(x+2y)-1 \right)y'=-2\left(x+2y+1 \right)$$
Divide through by $$4(x+2y)-1$$:
$$y'=-\frac{2\left(x+2y+1 \right)}{4(x+2y)-1}$$
Now, we want to equate this to the slope $m$ of the given line:
$$4x+3y=2$$
which we see is:
$$m=-\frac{4}{3}$$
And so we have:
$$\frac{2\left(x+2y+1 \right)}{4(x+2y)-1}=\frac{4}{3}$$
Dividing through by 2 and cross-multiplying yields:
$$3x+6y+3=8x+16y-2$$
Collect like terms:
$$5=5x+10y$$
Divide through by 5 and arrange as:
$$x=1-2y$$
Now, substituting for $x$ into the original equation, we obtain:
$$(1-2y+2y)^2+2(1-2y)-y-3=0$$
Solving for $y$, we find:
$$1+2-4y-y-3=0$$
$$y=0\implies x=1$$
Now, we have the point of tangency $(1,0)$ and the slope $$m=-\frac{4}{3}$$, and so the point-slope formula gives is the equation of the tangent line:
$$y-0=-\frac{4}{3}(x-1)$$
In slope-intercept form, this is:
$$y=-\frac{4}{3}x+\frac{4}{3}$$
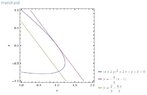
Here is a plot of the given curve, line and the tangent line:
View attachment 2109
Here is a link to the program I used to plot them:
(x+2y)^2+2x-y-3=0,y=(4/3)(1-x),y=(2-4x)/3, where x=0 to 2,y=-1 to 1 - Wolfram|Alpha