Find Tension in Horizontal Rope DE | Cylinder Mass & Angle θ

Click For Summary

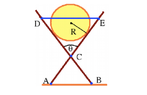
Discussion Overview

The discussion revolves around determining the tension in a horizontal rope (DE) that is part of a system involving a cylinder lodged between cross pieces at an angle θ. Participants explore the forces acting on the cylinder and the rails, focusing on static equilibrium and the application of free body diagrams (FBDs). The conversation includes technical reasoning and mathematical expressions related to the problem.

Discussion Character

  • Technical explanation
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • One participant outlines a general procedure for tackling statics problems, including identifying external forces and drawing FBDs.
  • Another participant identifies the weight of the cylinder as the primary downward force and discusses the reaction forces at the points of contact with the ground.
  • There is a discussion about the normal forces acting on the cylinder and how they relate to the tension in the rope.
  • Participants propose that the horizontal components of the normal forces may contribute to the tension, but there is uncertainty about how to derive the tension expression.
  • One participant suggests that the tension expression involves trigonometric functions of half of θ, while another participant expresses uncertainty about their own derived expression for tension.
  • There is mention of the forces acting on the rails, including the tension in the rope, normal forces, and the upward force from the ground.

Areas of Agreement / Disagreement

Participants generally agree on the need to analyze the forces acting on both the cylinder and the rails, but there is no consensus on the exact expression for tension or the method to derive it. Multiple competing views and uncertainties remain regarding the calculations and relationships between the forces.

Contextual Notes

Participants express uncertainty about the correct formulation of the tension and the role of various forces in the system. There are unresolved mathematical steps and dependencies on the definitions of forces involved.

Ciaran
Messages
71
Reaction score
0
Hi there,

I have a question I'm unable to get properly started on:

A cylinder of radius R and mass m is lodged between cross pieces that make
an angle θ with each other, as shown in the diagram below. The cross pieces
of negligible mass are connected in point C, with lengths AC = BC = 2R and
CD = CE = 3R. Determine the tension in the horizontal rope DE. You may
assume smooth floor.

Any help would be much appreciated!
View attachment 4083
 

Attachments

  • Screen Shot 2015-03-08 at 19.06.54.png
    Screen Shot 2015-03-08 at 19.06.54.png
    4.4 KB · Views: 120
Physics news on Phys.org
Ciaran said:
Hi there,

I have a question I'm unable to get properly started on:

A cylinder of radius R and mass m is lodged between cross pieces that make
an angle θ with each other, as shown in the diagram below. The cross pieces
of negligible mass are connected in point C, with lengths AC = BC = 2R and
CD = CE = 3R. Determine the tension in the horizontal rope DE. You may
assume smooth floor.

Any help would be much appreciated!

Hi Ciaran!

Here's the procedure to tackle any problem in statics.

1. Make an inventory of the external forces.
2. Draw a Free Body Diagram (FBD). That is a diagram of the object with only the external forces.
3. Apply the equilibrium equations of statics: $\sum F_x=0, \sum F_y=0, \sum T = 0$.
4. Make an inventory of the internal forces on each part.
5. Draw an FBD of each part.
6. Apply the equilibrium equations of statics on each part: $\sum F_x=0, \sum F_y=0, \sum T = 0$.

Which external forces can you identify?
Can you already say something about their sizes?
 
Hello again! I know the weight of the system will be the weight of the mass, m and that a reaction force will be split evenly and applied to either bit touching the ground. So it obviously isn't moving in the x or y direction. It's internally, I'm not sure how to deal with the contact forces between the mass and the cross rails.
 
Ciaran said:
Hello again! I know the weight of the system will be the weight of the mass, m and that a reaction force will be split evenly and applied to either bit touching the ground. So it obviously isn't moving in the x or y direction. It's internally, I'm not sure how to deal with the contact forces between the mass and the cross rails.

Good.

Let's give them a name. Let's say G is the force of gravity on the cylinder.
Then at A and B we will have an upward force of G/2 each, yes?
At A and B the horizontal component of force is 0, since the floor gives no friction.
That takes care of steps 1 and 3 and we've been sort of skipping step 2.

Where the rail touches the cylinder, there will be a normal force, perpendicular to the rail.
There won't be friction (parallel to the rail) because the cylinder cannot move/slide along the rail.

If we only look at the cylinder, which forces act on it?
What are their sizes?
 
The only force on the cylinder is G vertically downwards so this must be countered by the two forces from the cross rails, radially?
 
Ciaran said:
The only force on the cylinder is G vertically downwards so this must be countered by the two forces from the cross rails, radially?

Yes. Let's call them N, which is short for normal force.
 
Then the components that are horizontal will provide the tension?
 
Ciaran said:
Then the components that are horizontal will provide the tension?

No, we're not there yet.
The tension force does not work on the cylinder, it works on the rail.
To find the tension, first we need the normal force.

I suggest to try and draw an FBD for the cylinder, and also one for the rail.
We'll need them.
 
My FBD for the cylinder has 3 forces- gravity vertically downwards, and 2 radial forces 'inwards'. And for the rail there are 2 forces, each acting 'outward' due to each side of the rails being pulled down by the mass?
 
  • #10
Ciaran said:
My FBD for the cylinder has 3 forces- gravity vertically downwards, and 2 radial forces 'inwards'.

Good!

And for the rail there are 2 forces, each acting 'outward' due to each side of the rails being pulled down by the mass?

On one rail there is indeed 1 outward acting force by the cylinder.
There are 3 more forces...
 
  • #11
The weight of the rail? But it's considered negligible. And contact forces from where it touches two other rails.
 
  • #12
Ciaran said:
The weight of the rail? But it's considered negligible. And contact forces from where it touches two other rails.

No, not the weight of the rail.

Each rail has 4 forces acting on it:
1. The tension of the rope. Let's call it T.
2. The normal force of the cylinder, which I've already called N.
3. The force of the other rail where it is connected in point C. Let's call it R (for rail).
4. The upward force of the floor, which is G/2, since it's the only external force to counter the weight G of the cylinder.
 
  • #13
I understand that, yes. I'm just not sure about putting it all together. Have you an expression for the tension? I have one but it seems rather complicated and I'm not sure my method was correct. Does the answer involve secant and tangents of half of theta?
 
  • #14
Ciaran said:
I understand that, yes. I'm just not sure about putting it all together. Have you an expression for the tension? I have one but it seems rather complicated and I'm not sure my method was correct. Does the answer involve secant and tangents of half of theta?

Yes, it involves a couple of trigonometric functions of half of theta.
 
  • #15
It's not T= (1/6R)(R_N sec(theta/2))+ (1/3)Gtan(theta/2) is it? Where R_N is the radial force, R the radius of the cylinder and G as discussed before. Apologies for the typing- I'm not exactly an expert in using the software for equations!
 
  • #16
Ciaran said:
It's not T= (1/6R)(R_N sec(theta/2))+ (1/3)Gtan(theta/2) is it? Where R_N is the radial force, R the radius of the cylinder and G as discussed before. Apologies for the typing- I'm not exactly an expert in using the software for equations!

I have something similar but not the same, and in particular I evaluated $R_N$.

As for "using the software for equation", just put a dollar on each side of an equation. That should do the trick.
And if you want to be a bit more fancy, put a backslash (\) in front of some of the symbols like \theta and \tan.
 

Similar threads

Tension problem calculate theta
  • · Replies 4 ·
Replies
4
Views
2K
Tension in a deformed cylindrical bag on a surface
  • · Replies 18 ·
Replies
18
Views
2K
What are the tension and angle of support rope for a cylinder about to slip?
  • · Replies 18 ·
Replies
18
Views
2K
Tension of string joining two crossed sticks
  • · Replies 25 ·
Replies
25
Views
3K
Calculating Tension in a Telephone Wire with Mass and Angle
  • · Replies 5 ·
Replies
5
Views
3K
Tension in a rope placed on a cone
  • · Replies 7 ·
Replies
7
Views
2K
What is the angle θ between the tow rope and the center line
  • · Replies 2 ·
Replies
2
Views
2K
What is the tension in the rope DE?
  • · Replies 2 ·
Replies
2
Views
2K
Finding Tension force in a SHM Pendulum
  • · Replies 4 ·
Replies
4
Views
3K
Tension and Angle Analysis for Traction in a Broken Leg
  • · Replies 3 ·
Replies
3
Views
14K